Section 6: Matrix multiplication

The cs61-sections/s06 directory contains a program called matrixmultiply (source in matrixmultiply.cc). This program creates two random square matrices, multiplies them together, prints some information about their product, then exits.

In the handout code, matrixmultiply-base.cc and matrixmultiply.cc do exactly the same task. Your first job is to transform the matrixmultiply.cc version so that it runs as fast as possible, while producing almost exactly the same results as the original for all arguments. Your second job is to explain your results by reasoning about the processor cache.

Processor cache

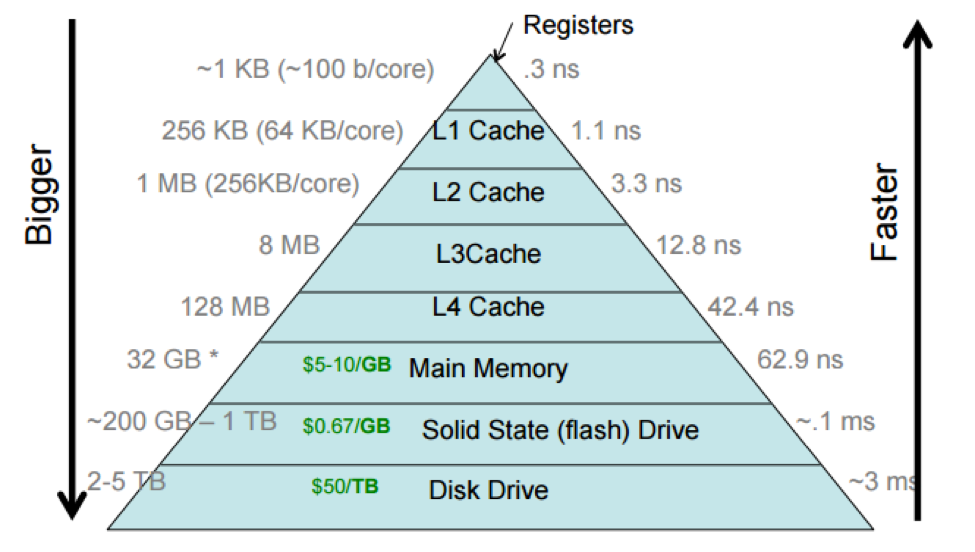
Modern processors access all primary memory through the medium of cache memory. This kind of memory is located physically closer to the processor than primary memory. Shorter wires means faster access: the closest cache memory is ~60x faster for the processor to access than primary memory. But there is also much less space available close to the processor, and cache memory can use a different technology than primary memory. So cache memory is smaller and more expensive than primary memory.

Cache memory is organized into aligned blocks called cache lines. Common cache line sizes are 64 bytes or 128 bytes.

To access an address in primary memory, a processor obtains a lock on the surrounding cache line (preventing other processors from modifying it), then moves the cache line into the cache.

Matrix multiplication background

A matrix is a 2D array of numbers. An \(m\times n\) matrix has \(m\) rows and \(n\) columns; the value in row \(i\) and column \(j\) is written \(m_{ij}\), or, in more C-like notation, \(m[i, j]\) or \(m[i][j]\).

A square matrix has the same number of rows and columns: \(m = n\).

The product of two matrices \(a\) and \(b\), written \(a \times b\) or \(a \ast b\), is calculated by the following rules.

1. \(a\) must have the same number of columns as \(b\) has rows.
2. If \(a\) has dimensions \(m\times n\), and \(b\) has dimensions \(n\times p\), then \(c = a \times b\) has dimensions \(m \times p\): it has \(a\)’s row count and \(b\)’s column count.

3. If \(c = a \times b\), then

   \[ c_{ij} = \sum_{0\leq k < n} a_{ik}b_{kj}. \]

Some pictures might help. Here’s how the dimensions work:

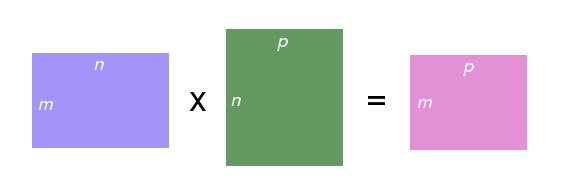
And here’s the values used to compute element \(c_{ij}\) of the destination matrix:

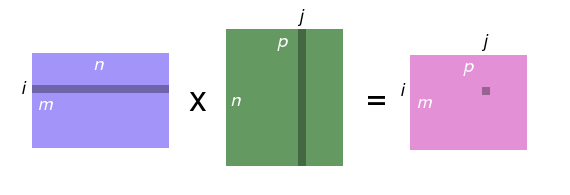
Matrixes in most languages are stored in row-major order. That means that we store the matrix in a single array, where the values for each row are grouped together. For instance, if \(a\) were a 4x4 square matrix, we’d store its (zero-indexed) elements in this order:

 0. a[0,0]
 1. a[0,1]
 2. a[0,2]
 3. a[0,3]
 4. a[1,0]
 5. a[1,1]
…
14. a[3,2]
15. a[3,3]

Thus, element \(a_{ij}\) is stored in array index a[i*NCOLS + j], where NCOLS is the number of columns (here, 4).

Your task

Once you get the “aha” insight you should be able to make matrix_multiply take no more than 0.1x the time of the base, while producing statistics that are 0% off.

Followup questions—answering them will demonstrate your understanding of processor caches:

1. Find the fastest matrix multiplier you can.
2. Find the slowest matrix multiplier you can.
3. Explain why these multipliers are fast and slow, referring to processor cache design.
4. Find a fast matrix multiplier that uses sqmatrix::transpose and one that does not.
5. Speed up sqmatrix::transpose if you can.
6. Find a radically faster matrix multiplier that relies on a library such as BLAS.

Note: You can copy matrixmultiply.cc as many times as you like. If you use filenames like matrixmultiply-magic.cc, the makefile will generate binaries like matrixmultiply-magic.

And some other followup questions:

1. If you run ./matrixmultiply -n N several times with the same N, you should notice that the corner statistics all stay about the same—even though the input matrices are being initialized randomly, and differently, each time. Why?