Storage 4: Processor caches and forking

Overview

In this lecture, we work through some examples of processor cache performance and transition to the process control unit.

Full lecture notes on storage — Textbook readings

Processor cache

• Processor caches divide primary memory into blocks of ~64 aligned bytes
  • 128 bytes on some machines
• Processor implements prefetching strategies
  • Sequential access often beneficial
  • User can help: prefetch instruction

accessor.cc

• Initialize array of N integers
• Sum up N elements of the array in one of three orders
  • -u (up order): 0…(N-1)
  • -d (down order): (N-1)…0
  • -r (random order): N random choices from [0, N-1)

Question

• What is the relative speed of these orders, and why?

list-inserter.cc

• Initialize sorted linked list of N integers
• Insert N elements in one of three orders
  • -u (up order): 0…N-1
  • -d (down order): N-1…0
  • -r (random order): N random choices from [0, N-1)

Question

• What is the relative speed of these orders, and why?

Machine learning

Machine learning Matrix multiplication

• Matrix is 2D array of numbers
• $m\times n$ matrix $M$ has $m$ rows and $n$ columns
  • $M_{ij}$ is the value in row $i$ and column $j$
• Product of two matrices $C = A \times B$
  • If $A$ is $m\times n$, then $B$ must have dimensions $n\times p$ (same number of rows as $A$ has columns), and $C$ has dimensions $m \times p$
  • $C_{ij} = \sum_{0\leq k < n} A_{ik}B_{kj}$

Pictorial matrix multiplication

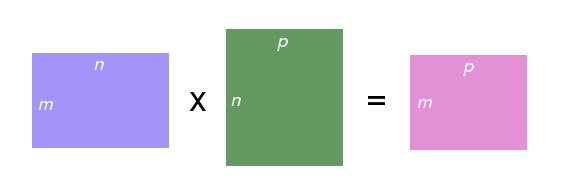
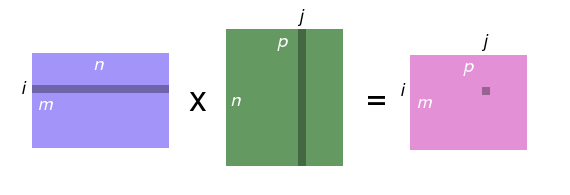
Matrix storage

• How to store a 2D matrix in “1D” memory?
• Row-major order
  • Store row values contiguously in memory
• Single-array representation
  • MxN matrix stored in array m[M*N]
  • Matrix element $M_{ij}$ stored in array element m[i*N + j]
  • 4x4 matrix: $A_{0,0}$ := a[0]; $A_{0,1}$ := a[1]; $A_{0,2}$ := a[2]; …; $A_{3,2}$ := a[14]; $A_{3,3}$ := a[15]

Implementing matrix multiplication

    // clear `c`
    for (size_t i = 0; i != c.size(); ++i) {
        for (size_t j = 0; j != c.size(); ++j) {
            c.at(i, j) = 0;
        }
    }

    // compute product and update `c`
    for (size_t i = 0; i != c.size(); ++i) {
        for (size_t j = 0; j != c.size(); ++j) {
            for (size_t k = 0; k != c.size(); ++k) {
                c.at(i, j) += a.at(i, k) * b.at(k, j);
            }
        }
    }

Question

• Can you speed up matrixmultiply.cc by 10x?

Forking, piping, and stdio

• fork1
• fork2
• fork3
  • ./fork3
  • ./fork3 | less
• forkmix