Section 12: Threads and lock granularity

In the first part of section, we’ll spend some time on some simple thread examples, working through ways of enforcing ordering through atomics, mutexes, and condition variables. Then we turn to the problem set, discussing different coarse-grained and fine-grained synchronization designs. After a discussion of fancy mutexes, there are some poop jokes.

Three threads

Recall that std::thread's constructor takes the name of the function to run on the new thread and any arguments, like std::thread t(func, param1, ...). Given a thread t, t.join() blocks the current thread until thread t terminates. t.detach() sets the t thread free—it can no longer be joined. Each thread object must be detached or joined before it goes out of scope (is destroyed).

QUESTION. What can this code print, and how many threads might run concurrently during its execution? (sample01.cc)

int main() {
    for (int i = 0; i != 3; ++i) {
        std::thread t(printf, "%d\n", i + 1);
        t.join();
    }
}

This can only print 1\n2\n3\n. Each line is printed in a separate thread, but there are never more than 2 threads running concurrently, the main thread and a separate thread running printf. The main function waits for each printf thread to complete before going to the next round of the loop.

QUESTION. What can this code print, and how many threads might run concurrently during its execution? (sample02.cc)

int main() {
    for (int i = 0; i != 3; ++i) {
        std::thread t(printf, "%d\n", i + 1);
        t.detach();
    }
}

This code will print some subset of the lines 1 2 3, in any order, and with any number of those lines left out—because when the main thread exits (by returning from main) all other threads are killed too. Up to four threads might be running concurrently.

QUESTION. What can this code print? (sample03.cc)

int main() {
    for (int i = 0; i != 3; ++i) {
        std::thread t(printf, "%d\n", i + 1);
    }
}

When the t thread goes out of scope without having been joined or detached, undefined behavior occurs. This isn’t a valid program and as such can print anything.

Counting to three

We now turn to this code, in counting.cc.

#include <thread>
#include <mutex>
#include <condition_variable>
#include <cstdio>

/* G1 */

void counter(int n) {
    /* C1 */
    printf("%d\n", n + 1);
    /* C2 */
}

int main() {
    /* M1 */
    std::thread t1(counter, 0);
    std::thread t2(counter, 1);
    std::thread t3(counter, 2);
    /* M2 */
    t3.join();
    t2.join();
    t1.join();
}

EXERCISE. What can this code print, and how many threads might run concurrently during its execution?

It can print 1 2 3 in any order, running up to 4 concurrent threads. However, it will not print subsets of 1 2 3—it will always print three lines—because each of the threads is joined before the main thread exits.

In the remaining exercises, we will synchronize this code so that it always prints 1\n2\n3\n, in that order. (The resulting code might as well run in a single thread—all useful work is performed by one thread at a time—but that’s OK for our purposes.)

Counting with atomics

EXERCISE. Use atomic variables to ensure that counting.cc always prints 1\n2\n3\n. There must be no data races. You should add code only in the marked locations (G1, C1, C2, M1, and/or M2). In particular, you should not reorder the join calls.

This is a synchronization problem. We ensure that threads execute in a specific order by introducing shared state on which the threads coordinate. But when shared state exists, accessing it safely requires synchronization.

As you design your synchronization state and code, think about the purpose served by the shared state that coordinates these threads. Discussion questions:

1. Describe that purpose at a high level.
2. How many atomic variables are required to represent this state? Are there different coordination designs with different numbers of atomic variables?
3. Can these atomic variables be local variables within counter, or must they be located elsewhere? Why?

1. A simple model is that we need “phase” information that indicates what thread should print next. In the first phase (phase 0), thread t1 gets permission to print, prints, and then advances the phase to 1. Then, in the second phase, thread t2 gets permission to print, prints, and then advances the phase to 2. And so on.

   There are other models too. For instance, you could model three different “permission” states, where each thread has separate state indicating whether it has permission to print. Each thread will give the next thread permission to print when it is done.

2. One atomic variable can model phase information; three atomic variables are required to model permission information.

3. The variables must not be local variables within counter, for they are used to coordinate different threads running counter. Given the constraints of the problem, the atomics must be global. (If we could change the arguments to counter, they could be local within main.)

Here is code implementing the “phase” model:

G1:
    std::atomic<int> phase = 0;
C1:
    while (phase != n) {
    }
C2:
    ++phase;

Here is code implementing the “permission” model:

G1:
    std::atomic<int> permission[3] = {1, 0, 0};
C1:
    while (!permission[n]) {
    }
C2:
    if (n < 2) {
        permission[n + 1] = true;
    }

QUESTION. Does your atomics-based solution use blocking or polling?

(Recall that blocking is when a thread waits in a non-runnable state. This can happen, for example, if the thread calls a system call like usleep, or waitpid without WNOHANG; the calling thread will not run until the system call completes, leaving the operating system free to do other work. Polling is when a thread waits in a runnable state—it continually loops back and checks to see if it can continue. This can happen, for example, if the thread calls waitpid with WNOHANG, in a loop.)

All our atomics-based solutions use polling: while (phase != n) or while (!permission[n]). Atomics offer no blocking functionality—we must use other synchronization objects for that.

Counting with mutexes

QUESTION. The following code using std::mutex is suspicious—very likely to be incorrect. Describe why, and suggest how to fix this problem.

std::mutex m;
int phase;
...
m.lock();
while (phase != 1) {
}
m.unlock();

The phase global variable appears to be protected from concurrent modification by the mutex m. (Otherwise, why would we acquire m before accessing phase?) But if phase is protected from concurrent modification, then the while (phase != 1) loop might run forever! If the other code is correct, then no other thread can modify phase while this thread holds the mutex.

The natural way to fix problems like this is to release the mutex m so that other threads get the chance to modify the shared state. A condition variable wait can do this, or you can “pulse” the mutex:

m.lock();
while (phase != 1) {
    m.unlock();
    /* other threads get a chance to run here, between `unlock` and `lock` */
    m.lock();
}
m.unlock();

EXERCISE. Change counting.cc to use synchronize using mutexes. Do not use condition variables or atomics.

It’s possible to implement either the phase model or the permission model using mutexes. One mutex can protect the phase, or the set of all three permissions; or there can be three mutexes, one per permission. In each case we need to use the mutex “pulsing” trick above.

First, using phases:

G1:
    int phase = 0;
    std::mutex m;
C1:
    m.lock();
    while (phase != n) {
        m.unlock();
        m.lock();
    }
C2:
    ++phase;
    m.unlock();

Next, using one mutex protecting all three permissions:

G1:
    int permission[3] = {1, 0, 0};
    std::mutex m;
C1:
    m.lock();
    while (!permission[n]) {
        m.unlock();
        m.lock();
    }
C2:
    if (n < 2) {
        permission[n + 1] = true;
    }
    m.unlock();

Finally, using three mutexes, one per permission:

G1:
    int permission[3] = {1, 0, 0};
    std::mutex m[3];
C1:
    m[n].lock();
    while (!permission[n]) {
        m[n].unlock();
        m[n].lock();
    }
    m[n].unlock();
C2:
    if (n < 2) {
        m[n + 1].lock();
        permission[n + 1] = true;
        m[n + 1].unlock();
    }

EXERCISE. Consider the solutions for the last exercise. Discuss different ways the synchronization can be moved around or changed without breaking functionality.

The mutual exclusion property mutexes provide can help us to reason about code rearrangement. State protected by a mutex will only be accessed while that mutex is locked, so two code arrangements that protect the same state, in the same order relative to externally-visible events (like data printed to standard output), have the same effects.

Some examples:

1. In the two solutions involving a single mutex, the printf call need not be protected by the mutex. The printf call doesn’t access the shared state relevant to that mutex, and phase and permission suffice to synchronize with the other threads. We can therefore release the mutex before printf, in C1, and reacquire it after, in C2:

   C1:
       m.lock();
       while (phase != n) {
           m.unlock();
           m.lock();
       }
       m.unlock();
   C2:
       m.lock();
       ++phase;
       m.unlock();
   

   C1:
       m.lock();
       while (!permission[n]) {
           m.unlock();
           m.lock();
       }
       m.unlock();
   C2:
       if (n < 2) {
           m.lock();
           permission[n + 1] = 1;
           m.unlock();
       }
   

2. Alternately, as long as the code does keep the mutex continually acquired while calling printf, it’s possible to change the phase or permission in C1, before printf. Mutual exclusion will ensure other threads will not observe the changed state until after the mutex unlocks, by which time printf has executed.

   C1:
       m.lock();
       while (phase != n) {
           m.unlock();
           m.lock();
       }
       ++phase;
   C2:
       m.unlock();
   

   C1:
       m.lock();
       while (!permission[n]) {
           m.unlock();
           m.lock();
       }
       if (n < 2) {
           permission[n + 1] = 1;
       }
   C2:
       m.unlock();
   

3. It’s also possible to modify the three-mutex version, for instance to acquire both mutexes in C1.

   C1:
       m[n].lock();
       while (!permission[n]) {
           m[n].unlock();
           m[n].lock();
       }
       if (n < 2) {
           m[n + 1].lock();
           permission[n + 1] = true;
       }
       m[n].unlock();
   C2:
       if (n < 2) {
           m[n + 1].unlock();
       }
   

QUESTION. Does your mutex-based solution use blocking or polling?

Just like the atomics-based solution, this uses polling! The mutex pulsing, which is necessary for correctness, makes this code polling-based.

Counting with condition variables

EXERCISE. Change counting.cc to use synchronize using mutexes and condition variables. Do not use atomics.

It’s possible to implement either the phase model or the permission model using condition variables. One condition variable can represent any change to phase or permission, or we can implement one condition variable per phase or permission.

First, using phases and one condition variable:

G1:
    int phase = 0;
    std::mutex m;
    std::condition_variable_any cv;
C1:
    m.lock();
    while (phase != n) {
        cv.wait(m);
    }
C2:
    ++phase;
    m.unlock();
    cv.notify_all();

Then, using phases and three condition variable:

G1:
    int phase = 0;
    std::mutex m;
    std::condition_variable_any cv[3];
C1:
    m.lock();
    while (phase != n) {
        cv[n].wait(m);
    }
C2:
    ++phase;
    if (phase < 3) {
        cv[phase].notify_all();
    }
    m.unlock();

One mutex and condition variable for all three permissions:

G1:
    int permission[3] = {1, 0, 0};
    std::mutex m;
    std::condition_variable_any cv;
C1:
    m.lock();
    while (!permission[n]) {
        cv.wait(m);
    }
C2:
    if (n < 2) {
        permission[n + 1] = true;
    }
    m.unlock();
    cv.notify_all();

One mutex and three condition variables, one per permission:

G1:
    int permission[3] = {1, 0, 0};
    std::mutex m;
    std::condition_variable_any cv[3];
C1:
    m.lock();
    while (!permission[n]) {
        cv[n].wait(m);
    }
C2:
    if (n < 2) {
        permission[n + 1] = true;
        cv[n + 1].notify_all();
    }
    m.unlock();

Three mutexes, one per permission, and one condition variable for all permission changes:

G1:
    int permission[3] = {1, 0, 0};
    std::mutex m[3];
    std::condition_variable_any cv;
C1:
    m[n].lock();
    while (!permission[n]) {
        cv.wait(m[n]);
    }
    m[n].unlock();
C2:
    if (n < 2) {
        m[n + 1].lock();
        permission[n + 1] = true;
        m[n + 1].unlock();
        cv.notify_all();
    }

Three mutexes and three condition variables, one each per permission:

G1:
    int permission[3] = {1, 0, 0};
    std::mutex m[3];
    std::condition_variable_any cv[3];
C1:
    m[n].lock();
    while (!permission[n]) {
        cv[n].wait(m[n]);
    }
    m[n].unlock();
C2:
    if (n < 2) {
        m[n + 1].lock();
        permission[n + 1] = true;
        m[n + 1].unlock();
        cv[n + 1].notify_all();
    }

QUESTION. Does your condition-variable-based solution use blocking or polling?

Finally we have a blocking-based solution!

QUESTION. Which of these solutions use fine-grained synchronization (as opposed to coarse-grained synchronization)?

Recall that fine-grained synchronization is when a program involves many synchronization objects, each protecting a relatively small amount of state (or, in the case of condition variables, representing a specific condition). Coarse-grained synchronization is when a program involves relatively few synchronization objects, each protecting a larger amount of state (or representing a more general condition). In programs with coarse-grained synchronization, only a small number of threads can execute concurrently (because each thread typically acquires a coarse-grained mutex that locks out most other threads). In programs with fine-grained synchronization, a larger number of thread can execute concurrently (each thread may acquire several mutexes, but other threads can proceed if they operate on different state and therefore acquire different mutexes).

The finest-grained solution involves three mutexes and three condition variables. However, for this problem, where only one thread at a time can perform useful work, coarse-grained synchronization is a perfectly sensible synchronization design.

Breakout synchronization

In the problem set, your task involves implementing non-coarse-grained synchronization for a “breakout” game, in which many balls, each handled by a single thread, carom around a rectangular field.

To design a synchronization strategy for a task, it’s necessary to enumerate the shared state required for that task—especially the modifiable shared state. To avoid data races, any modifiable shared state must be accessed in a synchronized manner—generally while protected by a mutex, though potentially through atomics.

The shared state in the breakout game consists of:

• The board metadata: its width and height, and the number of collisions.
• Other metadata: the delay times delay and warp_delay and the number of running threads.
• For each board cell, its state (type, strength, warp, ball).
• For each ball, its position (x,y).
• For each ball, its direction (dx,dy).
• For each ball, its state (stopped/not stopped).
• For each warp tunnel end, its position (x,y).
• For each warp tunnel end, its contents (an optional ball).

A breakout game with B threads and W warp-tunnel ends has (B + W) threads. The ball threads move balls around the board, while the warp-tunnel threads warp balls from position to position.

QUESTION. What parts of this state are read-only after initialization (i.e., they are only modified while the game is being initialized, before any ball or warp threads begin)? Do these parts of the state require synchronization to access? (You can figure this out by examining the code!)

The board width, board height, delay times, cells’ warp-tunnel ends, and warp tunnels’ x,y positions are read-only after initialization, and do not need any synchronization to access. Everything else can be modified after initialization and requires some synchronization.

QUESTION. Which threads might modify a ball’s x,y position? (Again, you can figure this out by examining the code.)

A ball’s x,y position may be modified by (1) the thread handling that ball, and (2) any thread handling a warp tunnel.

QUESTION. Which threads might modify a ball’s dx,dy direction?

A ball’s dx,dy direction may be modified by the thread handling that ball (for instance, if the ball hits an obstacle). However, thanks to collisions, any ball thread might modify any ball’s dx,dy direction. This happens when one ball touches a cell containing another ball. Warp-tunnel threads do not modify ball directions.

QUESTION. Assume you were implementing a coarse-grained locking strategy where a single mutex protected all shared state. How would you modify ball_thread to implement correct synchronization? Would you need to pulse the mutex?

Yes, you would need to pulse the mutex to allow balls to take turns! It would be best to lock the mutex only around the call to b->move(). Only b->move() accesses shared state; the return value mval is local state, inaccessible from other threads and not requiring synchronization. It is also unwise to hold a mutex while blocking, for instance during usleep.

DISCUSSION QUESTION. Discuss in general terms how you might build a fine-grained synchronization strategy for the breakout board. Don’t worry about warps at first. More specifically:

1. Would it make more sense to implement one mutex per ball, or one mutex per board position (x,y)? (Recall that the goal of fine-grained synchronization is for threads to acquire a small number of mutexes, and for different threads to typically acquire different mutexes.)

2. How would it be possible to implement a strategy with fewer than one mutex per board position, but two or more mutexes for the board as a whole?

3. Would it make more sense to implement one condition variable per ball, or one condition variable per board position?

Here are our answers!

1. It would make more sense to implement one mutex per board position. A positional mutex protects the state of that cell plus the state of any ball at that position. Since balls interact only when they’re in adjacent positions, a ball thread could acquire a limited set of position-based mutexes (those corresponding to adjacent positions) in order to protect its state from concurrent access. Furthermore, the ball thread can safely examine its own position before acquiring any mutex. However, since any ball might interact with any other ball, and balls can change position arbitrarily, given per-ball mutexes, a ball thread would have to acquire all ball mutexes before checking for collisions. That’s equivalent to coarse-grained synchronization.

2. Sure! One could, for example, implement one mutex per row, or one mutex per column, or one mutex per 5x5 region.

   (We find that per-row/column designs are simplified by allocating additional mutexes for the “boundary” rows/columns that are just beyond the board, leading to (height+2) or (width+2) mutexes total. We also find that some designs are simplified by the use of std::recursive_mutex; see below.)

3. Condition variables are useful to wait for a condition in a blocking, rather than polling, fashion. The ball_thread waits in polling fashion in one situation, namely that the ball is stopped (e.g., in a sticky cell and waiting for a collision). This condition is naturally represented by a per-ball condition variable. (It could also be represented by a per-position condition variable, but that might complicate the interaction between warp tunnels—which change ball positions—and ball threads.)

DISCUSSION QUESTION. In the handout code, a warp thread can change a ball’s x,y position. Can you change the code so that the warp thread does not change ball positions—instead, the ball’s own thread changes its position? Why might this be useful for synchronization purposes?

Yes, it is possible to change the code so that the ball’s own thread changes its position. Before discussing how, we discuss why.

As we saw above, it makes the most sense in fine-grained synchronization to protect a ball’s state using the mutex corresponding to its position (or a region containing its position). But this is self-referential, because we must access the ball’s position in order to lock the mutex that protects its position!

Absent warp tunnels, this self-referentiality causes no problems: no other threads modify the position, so it’s safe for the ball’s own thread to read that position, even before it acquires the corresponding mutex. (Concurrent read-only accesses don’t cause data races.) But warp tunnels break that invariant. When warp threads modify ball positions, data races are introduced with the ball thread’s code that selects position-based mutexes to lock!

To recover the desirable quality that ball positions are read-only outside a ball’s own thread, you could introduce a signaling mechanism between warp threads and ball threads. The part of the warp thread that places a ball on the board, namely this:

assert(!cdest.ball);
cdest.ball = b;
b->x = w->x;
b->y = w->y;
b->stopped = false;

could be moved to ball_thread, and triggered by warp_thread. For instance, you could add a member bool unwarp = false to pong_ball, and set b->unwarp = true in warp_thread (protected by the corresponding positional mutex). The unwarping code would run in ball_thread when b->unwarp == true.

Fancy mutexes

std::recursive_mutex is like a normal mutex, but a thread that holds a lock may recursively acquire it again (as long as they recursively release it the same number of times). This might be useful if you need to acquire several locks, and sometimes some of those locks might actually be the same lock: with recursive locks, you don't need to keep track of which ones you already hold, to avoid acquiring the same lock twice.

std::shared_mutex is an instantiation of a different kind of lock altogether: a readers-writer lock, or a shared-exclusive lock. The idea behind this kind of lock is that rather than just have one level of access—mutual exclusion—there are two levels of access: shared access and exclusive access. When a thread holds the lock with shared access, that guarantees that all other threads that hold the lock have shared access. When a thread holds the lock with exclusive access, that guarantees that it is the only thread to have any kind of access. We call this a readers-writer lock because the two levels of access often correspond to multiple reader threads, which require the shared data not to change while they're accessing it, but don't modify it themselves; and a single writer thread, which needs to be the only thread with access to the data it's modifying. You do not need the functionality of std::shared_mutex for the problem set, and in fact it is not particularly helpful for this particular application.

std::mutex will likely suffice for this problem set, though std::recursive_mutex may simplify some logic.

std::lock avoids deadlock

C++ also defines some handy tools to acquire locks while avoiding deadlock. Instead of calling .lock() on the mutex itself, you can pass several mutexes as arguments to the function std::lock, which magically acquires the locks in an order that avoids deadlock. For example:

#include <mutex>

std::mutex a;
std::mutex b;

void worker1() {
    std::lock(a, b);
    ...
    a.unlock(); // the order of these doesn't matter,
    b.unlock(); // since unlocking can't cause deadlock
}

void worker2() {
    std::lock(b, a); // look ma, no deadlock!
    ...
    b.unlock();
    a.unlock();
}

...

std::unique_lock and std::scoped_lock unlock for you

The std::scoped_lock and std::unique_lock objects automate some aspects of locking, because they are capable of automatically unlocking. This is really convenient—it’s very easy to forget a call to unlock if a function has multiple return statements in it.

To use a scoped lock, you declare an object at the point where you would normally call lock(). This object is typically called a guard, since it exists to “guard” the lock. You must pass in a reference to the std::mutex that you intend to lock. For example, here’s a version of the increase function from above:

#include <mutex>

int i;
std::mutex m; // protects write access to i

void increase() {
    std::unique_lock guard(m);
    i++;
}

The declaration of guard will block until m can be locked, and then m is automatically unlocked when the function returns and guard goes out of scope (the variable stops existing). This is an instance of an idiom called Resource acquisition is initialization (RAII), which is the idea that an object's resources are automatically acquired and released by its constructor and destructor, which are triggered by scope.

Here’s how std::scoped_lock (which is the multi-lock version of std::unique_lock) would simplify the code above:

#include <mutex>

std::mutex a;
std::mutex b;

void worker1() {
    std::scoped_lock guard(a, b);
    ...
}

void worker2() {
    std::scoped_lock guard(b, a);
    ...
}

...

The std::unique_lock has .lock(), .try_lock(), and .unlock() member functions, in addition to the initialization/deinitialization style, and these can be useful sometimes. (The std::scoped_lock has no member functions at all: you can only use it by declaring it and then letting it go out of scope later.)

Bathroom synchronization

Ah, the bathroom. Does anything deserve more careful consideration? Is anything more suitable for poop jokes?

Bathroom 1: Stall privacy

In this exercise, the setting is a bathroom with K stalls numbered 0 through K–1. A number of users enter the bathroom; each has a preferred stall. Each user can be modeled as an independent thread that repeatedly calls the following code:

void user(int preferred_stall) {
    poop_into(preferred_stall);
}

Each user has a preferred stall that never changes, and two users should never poop_into the same stall at the same time.

You probably can intuitively smell that this bathroom model has a synchronization problem. Answer the following questions without referring to the solutions first.

Question: What synchronization property is missing?

Mutual exclusion (two users can poop into the same stall at the same time).

Question: Provide synchronization using a single mutex, i.e., using coarse-grained locking. Your solution should be correct (it should avoid gross conditions [which are race conditions in the context of a bathroom-themed synchronization problem]), but it need not be efficient. Your solution will consist of (1) a definition for the mutex, which must be a global variable, and (2) new code for user(). You don’t need to sweat the syntax.

std::mutex bmutex;
void user(int preferred_stall) {
    std::unique_lock guard(bmutex);
    poop_into(preferred_stall);
}

Question: Provide synchronization using fine-grained locking. Your solution should be more efficient than the previous solution. Specifically, it should allow the bathroom to achieve full utilization: it should be possible for all K stalls to be in use at the same time. You will need to change both the global mutex—there will be more than one global mutex—and the code for user().

std::mutex stall[K];
void user(int preferred_stall) {
    std::unique_lock guard(stall[preferred_stall]);
    poop_into(preferred_stall);
}

Bathroom 2: Stall indifference

The setting is the same, except that now users have no predetermined preferred stall:

void user() {
    int preferred_stall = random() % K;
    poop_into(preferred_stall);
}

Question: Adapt your solution from Bathroom 1 to work for this variant.

std::mutex stall[K];
void user() {
    int preferred_stall = random() % K;
    std::unique_lock guard(stall[preferred_stall]);
    poop_into(preferred_stall);
}

Question: As written, the user code picks a preferred stall and then waits for that stall to become available. This isn’t as efficient as possible, since multiple users might pick the same stall by chance. Write a synchronization solution where each user chooses any available stall. First, use a single mutex coupled with a global data structure representing stall occupancy.

std::mutex bmutex;
bool occupied[K];

void user() {
    int preferred_stall = -1;
    while (preferred_stall == -1) {
        std::unique_lock<std::mutex> guard(bmutex);
        for (int stall = 0; stall != K; ++stall) {
            if (!occupied[stall]) {
                preferred_stall = stall;
                occupied[stall] = true;
                break;
            }
        }
    }

    poop_into(preferred_stall);

    std::unique_lock<std::mutex> guard(bmutex);
    occupied[preferred_stall] = false;
}

Question: Repeat this function, but this time use multiple mutexes and no other global data structure.

std::mutex smutex[K];

void user() {
    while (true) {
        int preferred_stall = random() % K;
        if (smutex[preferred_stall].try_lock()) {
            poop_into(preferred_stall);
            smutex[preferred_stall].unlock();
            return;
        }
    }
}

Question: Compare these two implementations in terms of the number of std::mutex lock attempts it might take to poop.

The second solution may perform more synchronization calls, because it may make a synchronization call on many locked stalls before finding an unlocked stall. But the first solution performs a minimum of 4 synchronization calls, while the second solution performs a minimum of 2.

Question: These solutions implement a polling style. Why?

They repeatedly call try_lock, or they repeatedly call unlock+lock, while waiting for a stall to vacate.

Question: Implement a blocking implementation. You will need a condition_variable.

std::mutex bmutex;
std::condition_variable cv;
bool occupied[K];

int find_unoccupied_stall() {
    for (int i = 0; i != K; ++i) {
        if (!occupied[i]) {
            return i;
        }
    }
    return -1;
}

void user() {
    std::unique_lock<std::mutex> lock(bmutex);
    int preferred_stall;
    while (true) {
        preferred_stall = find_unoccupied_stall();
        if (preferred_stall != -1) {
            occupied[preferred_stall] = true;
            break;
        }
        cv.wait(lock);
    }
    lock.unlock();

    poop_into(preferred_stall);

    lock.lock();
    occupied[preferred_stall] = false;
    cv.notify_all();
    lock.unlock();
}

Bathroom 3: Pooping philosophers

To facilitate the communal philosophical life, Plato decreed that philosophy should be performed in a bathroom with K thrones and K curtains, arranged like so:

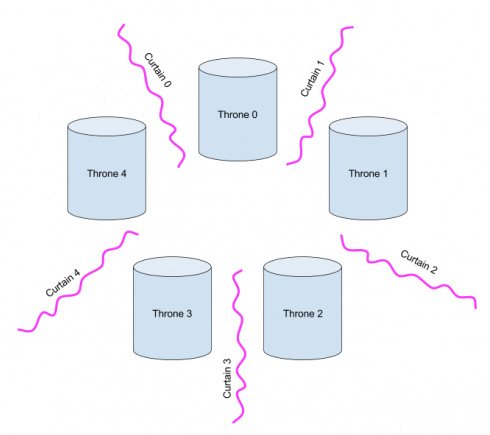
Each philosopher sits on a throne with two curtains, one on each side. The philosophers normally argue with one another. But sometimes a philosopher’s got to poop, and to poop one needs privacy. A pooping philosopher must first draw the curtains on either side; philosopher X will need curtains X and (X+1) mod K. For instance, here, philosophers 0 and 2 can poop simultaneously, but philosopher 4 cannot poop until philosopher 0 is done (because philosopher 4 needs curtain 0), and philosopher 1 cannot poop until philosophers 0 and 2 are both done:

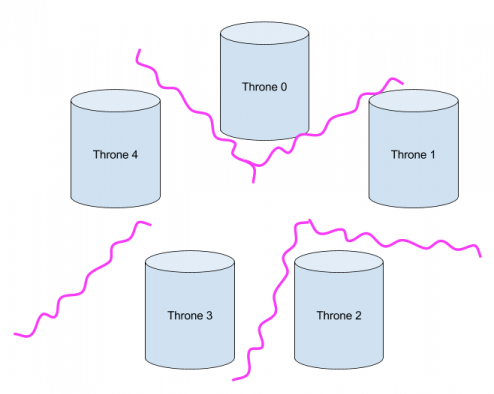
Question: In high-level terms, what is the mutual exclusion problem here—that is, what resources are subject to mutual exclusion?

Curtains. The mutual exclusion problem here is that each philosopher must have 2 curtains in order to poop, and a curtain can only be held by one philosopher at a time.

A philosopher could be described like this:

void philosopher(int x) {
    while (true) {
        argue();
        draw curtains x and (x + 1) % K;
        poop();
        release curtains x and (x + 1) % K;
    }
}

Question: Write a correctly-synchronized version of this philosopher. Your solution should not suffer from deadlock, and philosophers should block (not poll) while waiting to poop. First, use std::scoped_lock—which can (magically) lock more than one mutex at a time while avoiding deadlock.

std::mutex curtains[K];
void philosopher(int x) {
    while (true) {
        argue();
        std::scoped_lock guard(curtains[x], curtains[(x + 1) % K]);
        poop();
    }
}

Question: Can you do it without std::scoped_lock?

Sure; we just enforce our own lock order.

std::mutex curtains[K];
void philosopher(int x) {
    while (true) {
        argue();
        int l1 = std::min(x, (x + 1) % K);
        int l2 = std::max(x, (x + 1) % K);
        std::unique_lock<std::mutex> guard1(curtains[l1]);
        std::unique_lock<std::mutex> guard2(curtains[l2]);
        poop();
    }
}