Storage 2: Cache optimizations and coherence

Overview

In this lecture, we describe access costs and cache optimization strategies.

Full lecture notes on storage — Textbook readings

Storage hierarchy

• Modern computer software and hardware orchestrates many different data storage technologies into a unified whole
• Caching is implemented at many levels
• These technologies together are called the storage hierarchy or memory hierarchy

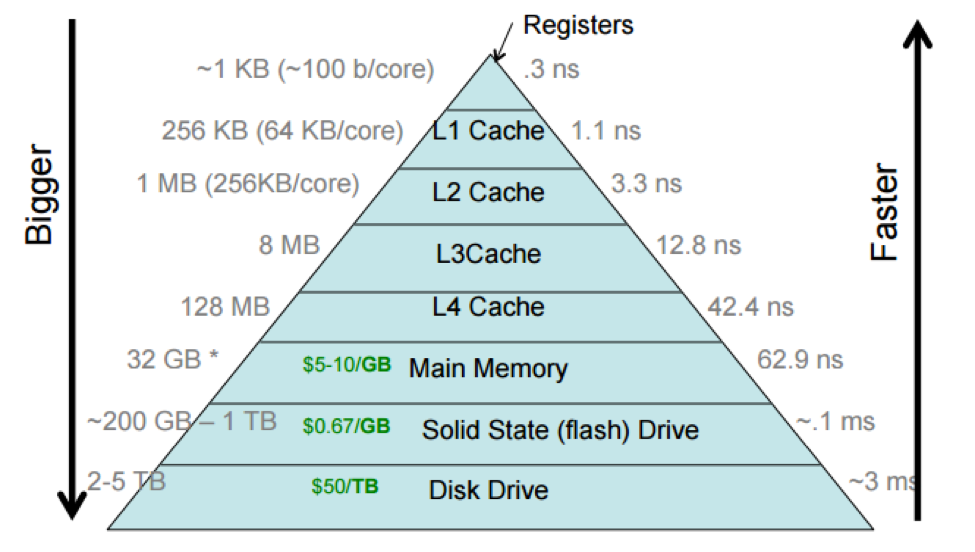
Systems cache examples

• Processor caches
  • Administered by: processor hardware (CPU/socket/motherboard)
  • Underlying storage: main memory (DRAM)
  • Fast storage: cache memory (SRAM)
• Buffer cache
  • Administered by: kernel
  • Underlying storage: durable media (flash, hard disk)
  • Fast storage: main memory (DRAM, physical memory)
• Stdio cache
  • Administered by: application library
  • Underlying storage: durable media via buffer cache
  • Fast storage: application memory
• Browser cache
  • Administered by: browser
  • Underlying storage: remote web sites over network
  • Fast storage: durable media

Expense of storage

• Expense is a major factor in the construction of computer systems
  • Faster technologies are often more expensive
  • Older, slower technologies are often cheaper
• The relative and absolute expenses of storage technologies may be the single thing about computer systems that has changed the most dramatically over time

Question

• How much more did a megabyte of memory cost in 1955, compared to now?
• How much more did a megabyte of hard disk storage cost in 1955, compared to now?

Historical costs of storage

Absolute costs ($/MB):

Year	Memory (DRAM)	Flash/SSD	Hard disk
~1955	$613,000,000		$9,290
1970	$1,090,000		$388
1990	$221		$8.13
2003	$0.134	$0.455	$0.00194
2010	$0.0283	$0.00358	$0.000108
2025	$0.004	$0.00005	$0.000039

Relative costs (relative to hard disk storage in 2025):

Year	Memory (DRAM)	Flash/SSD	Hard disk
~1955	15,700,000,000,000		238,000,000
1970	28,000,000,000		9,950,000
1990	5,670,000		208,000
2003	3,440	11,600	49.7
2010	727	91.8	2.79
2025	102	1.28	1.00

(Processor speed has also increased a lot—from 0.002 MIPS in 1951 to 750,000 MIPS now—but this is “only” 375,000,000x.)

Access cost framework

• C_N: Cost of accessing N units of data at once (N \geq 1)
  • Cost is often measured in terms of time (latency)
  • C_N = \infty if it is impossible to access N units at once
• As a rough estimate, many access costs are approximated by C_N = R + NU
  • R is the cost per request, independent of the number of units accessed by that request
  • U is the cost per unit

Example: System calls

• Consider the cost of a read(fd, buf, sz) system call
• Remember how stdio achieves benefits
• Assume read roughly obeys C_N = R + NU. Is R > U, or is R < U?

Beyond latency

• The performance of storage is best measured using two metrics
• Latency (delay): how many seconds it takes to complete a request
  • Units: seconds
  • Smaller latency is better
• Throughput: how many units of data can be moved per second
  • Units: bytes per second (or blocks per second, etc.)
  • Larger throughput is better

Relationship of latency and throughput

• For some storage technologies, latency and throughput are inverses
  • throughput = latency⁻¹
  • True random access
  • In the cost framework, R=0 and C_N = NU
• For other technologies, latency and throughput can diverge
  • For example, some technologies support parallel requests
  • Hard disk drive throughput: ~1–250 MiB/s
  • Hard disk drive latency: ~0.4–10 ms
  • SSD (flash drive) throughput: ~50–3000 MiB/s
  • SSD latency: ~30–100 µs
  • In the cost framework, R\gg 0

High-latency, high-throughput I/O

Access costs, latency, and throughput

• Assume per-request cost is much smaller than per-unit cost (R \ll U)
  • Example: main memory access
  • Then C_N \approx NU
  • Throughput per unit with N-unit requests = N/C_N \approx 1/U
  • Latency = C_1 \approx U
• Assume per-unit cost is much smaller than per-request cost (U \ll R)
  • Examples: system calls, reading/writing a disk drive
  • Then C_N \approx R
  • Throughput per unit with N-unit requests = N/C_N \approx N/R
  • Latency = C_1 \approx R
• Assume per-unit and per-request costs are comparable (neither dominates)
  • Example: network communication
  • Then C_N depends on both R and U

Reducing access costs

• Reduce number of requests
  • Avoid redundant requests
  • Do the same work in fewer requests

Cache optimizations

• Batching (read or write)
• Prefetching (read)
• Write coalescing (write)
• Parallel access (read or write)

Batching

• Combine multiple requests into one request
• Example: Read 4096 bytes in 1 request, instead of 1 byte 4096 times
• Reduces total per-request cost R

Prefetching

• Read data into a cache before it is needed
• Example: Assume sequential access; read bytes [d, d + 4096)
• Reduces number of requests

Write coalescing

• Delay writes to underlying storage until collecting several writes to cache
• Example: Assume a cache line is updated multiple times
  • Think a local variable updated in a loop, or multiple local variables in a cache line updated in close proximity
• Reduces number of requests

Parallel or background access

• Perform accesses in parallel with other work

Question

• How might these optimization strategies hurt performance?
• How might these optimizations change semantics (produce different observable results)?

Exploring performance of file access

• w-osbyte vs. w-osblock
• w-stdiobyte vs. w-stdioblock

Exploring performance of access patterns

• r-osbyte vs. r-osbyterev
• r-stdiobyte vs. r-stdiobyterev