Storage 2: Cache optimizations and coherence

Overview

In this lecture, we describe access costs and cache optimization strategies, then discuss cache coherence.

Full lecture notes on storage — Textbook readings

Cache

• A cache is an area of fast storage used to speed up access to underlying storage

Storage hierarchy

• Caches often make use of different technologies that store data
• These technologies often work together to form an effective unit called the storage hierarchy or memory hierarchy

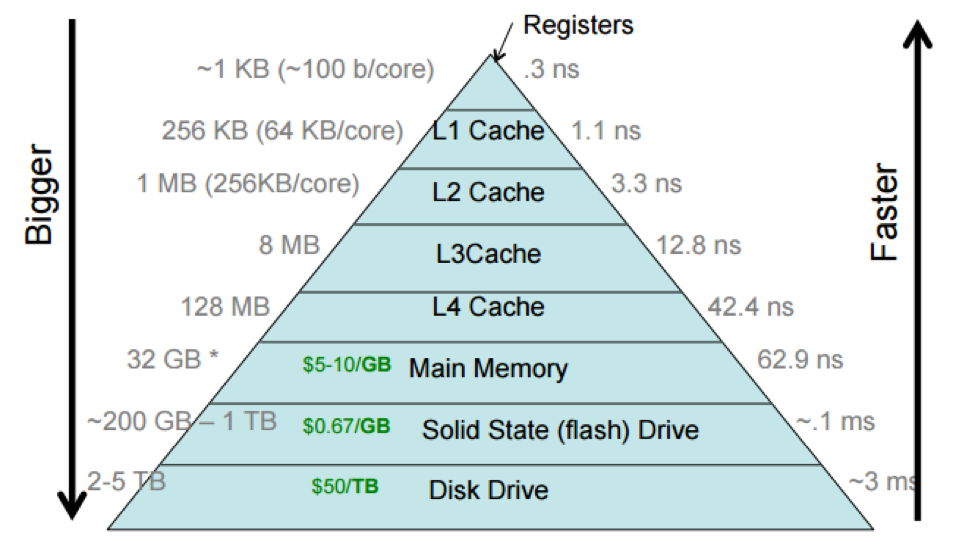
Systems cache examples

• Processor caches
  • Administered by: processor hardware (CPU/socket/motherboard)
  • Underlying storage: main memory (DRAM)
  • Fast storage: cache memory (SRAM)
• Buffer cache
  • Administered by: kernel
  • Underlying storage: durable media (flash, hard disk)
  • Fast storage: main memory
• Stdio cache
  • Administered by: application library
  • Underlying storage: durable media via buffer cache
  • Fast storage: main memory
• Browser cache
  • Administered by: browser
  • Underlying storage: remote web sites over network
  • Fast storage: durable media

Expense of storage

• Expense is a major factor in the construction of computer systems
  • Faster technologies are often more expensive
  • Older, slower technologies are often cheaper
• The relative and absolute expenses of storage technologies may be the single thing about computer systems that has changed the most dramatically over time

Question

• How much more did a megabyte of memory cost in 1955 relative to now?
• How much more did a megabyte of hard disk storage cost in 1955 relative to now?

Historical costs of storage

Absolute costs ($/MB):

Year	Memory (DRAM)	Flash/SSD	Hard disk
~1955	$411,000,000		$6,230
1970	$734,000		$260.00
1990	$148.20		$5.45
2003	$0.09	$0.305	$0.00132
2010	$0.019	$0.00244	$0.000073
2022	$0.0027	$0.000073	$0.000016

Relative costs (relative to hard disk storage in 2022):

Year	Memory	Flash/SSD	Hard disk
~1955	25,700,000,000,000		389,000,000
1970	45,900,000,000		16,300,000
1990	9,260,000		340,000
2003	5,600	19,100	82.5
2010	1,190	153	4.6
2022	168	4.6	1

(Processor speed has also increased a lot—from 0.002 MIPS in 1951 to 750,000 MIPS now—but this is “only” 375,000,000x.)

Performance of storage

• The performance of storage is best measured using two metrics
• Latency (delay): how many seconds it takes to complete a request
  • Units: seconds
  • Smaller latency is better
• Throughput: how many units of data can be moved per second
  • Units: bytes per second (or blocks per second, etc.)
  • Larger throughput is better

Relationship of latency and throughput

• For some storage technologies, latency and throughput are inverses
  • throughput = latency⁻¹
  • True random access
• For other technologies, latency and throughput can diverge
  • For example, some technologies support parallel requests
  • Hard disk drive throughput: ~1–250 MiB/s
  • Hard disk drive latency: ~0.4–10 ms
  • SSD (flash drive) throughput: ~50–3000 MiB/s
  • SSD latency: ~30–100 µs

High-latency, high-throughput I/O

Access cost framework

• C_N: Cost of accessing N units of data at once (N \geq 1)
  • Cost often means delay
  • C_N = \infty if it is impossible to access N units at once
• As a rough estimate, many storage costs are approximated by C_N = R + NU
  • R is the cost per request, independent of the number of units accessed by that request
  • U is the cost per unit

Financial examples

• ATM withdrawal out-of-network
  • $1 fee per transaction
  • Withdrawal limit of $400/day
• Let C_N represent the fee of withdrawing \$N
  • C_N = \mathord{?}
  • C_N = \begin{cases} 1 & \text{if } N \leq 400 \\ \infty & \text{otherwise}\end{cases}
  • R = 1, U = 0
• Credit card fees
  • $0 fee per transaction
  • 17%+ APR per month
• Let C_N represent the 1-month cost of a balance of \$N
  • C_N = \mathord{?}
  • C_N = 0.17N
  • R = 0, U = 0.17

Access costs, latency, and throughput

• If one unit of data is moved per request, and requests cannot execute in parallel, then throughput = latency⁻¹
• Assume per-request cost is much smaller than per-unit cost (R \ll U)
  • Example: main memory access
  • Then C_N \approx NU
  • Throughput per unit with N-unit requests = N/C_N \approx 1/U
  • Latency = C_1 \approx U
• Assume per-unit cost is much smaller than per-request cost (U \ll R)
  • Examples: system calls, reading/writing a disk drive
  • Then C_N \approx R
  • Throughput per unit with N-unit requests = N/C_N \approx N/R
  • Latency = C_1 \approx R
• Assume per-unit and per-request costs are comparable (neither dominates)
  • Example: network communication
  • Then C_N depends on both R and U

Reducing access costs

• Reduce number of requests
  • Avoid redundant requests
  • Do the same work in fewer requests

Cache optimizations

• Batching (read or write)
• Prefetching (read)
• Write coalescing (write)
• Parallel access (read or write)

Batching

• Combine multiple requests into one request
• Example: Read 4096 bytes in 1 request, instead of 4096 requests of 1 byte each
• Reduces total per-request cost R

Prefetching

• Read data into a cache before it is needed
• Example: Assume sequential access; read bytes [d, d + 4096)
• Reduces number of requests

Write coalescing

• Delay writes to underlying storage until collecting several writes to cache
• Example: Assume a cache line is updated multiple times
  • Think a local variable updated in a loop, or multiple local variables in a cache line updated in close proximity
• Reduces number of requests

Parallel or background access

• Perform accesses in parallel with other work

Question

• How might these optimization strategies hurt performance?
• How might these optimizations change semantics (produce different observable results)?

Exploring performance of file access

• w-osbyte vs. w-osblock
• w-stdiobyte vs. w-stdioblock

Exploring performance of access patterns

• r-osbyte vs. r-osbyterev
• r-stdiobyte vs. r-stdiobyterev