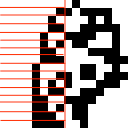Exercises not as directly relevant to this year’s class are marked with ⚠️.
DATAREP-1. Sizes and alignments
QUESTION DATAREP-1A. True or false: For any non-array type X, the
size of X (sizeof(X)) is greater than or equal to the alignment of
type X (alignof(X)).
QUESTION DATAREP-1B. True or false: For any type T, the size of
struct Y { T a; char newc; } is greater than the size of T.
QUESTION DATAREP-1C. True or false: For any types T1...Tn (with
n ≥ 1), the size of struct Y is greater than the size of struct X,
given:
struct X { T1 m1; ... Tn mn; };
struct Y { T1 m1; ... Tn mn; char newc; };
QUESTION DATAREP-1D. True or false: For any types T1...Tn (with
n ≥ 1), the size of struct Y is greater than the size of union X,
given:
union X { T1 m1; ... Tn mn; };
struct Y { T1 m1; ... Tn mn; };
QUESTION DATAREP-1E. Assume that structure struct Y { ... }
contains K char members and M int members, with K≤M, and
nothing else. Write an expression defining the maximum
sizeof(struct Y).
QUESTION DATAREP-1F. Given struct Z { T1 a; T2 b; T3 c; }, which contains no padding, what does (sizeof(T1) + sizeof(T2) + sizeof(T3)) % alignof(struct Z) equal?
QUESTION DATAREP-1G. Arrange the following types in increasing order by size. Sample answer: “1 < 2 = 4 < 3” (choose this if #1 has smaller size than #2, which has equal size to #4, which has smaller size than #3).
charstruct minipoint { uint8_t x; uint8_t y; uint8_t z; }intunsigned short[1]char**double[0]
DATAREP-2. Expression matching
QUESTION DATAREP-2A. Consider the following eight expressions:
msizeof(&m)-1m & -mm + ~m + 132 >> 2m & ~m1
For one unique value of m, those eight expressions can be grouped into four
matched pairs where the two expressions in each pair have the same value, and
expressions in different pairs have different values. What are the values of
the expressions for that m?
DATAREP-3. Hello binary
This problem locates 8-bit numbers horizontally and vertically in the following 16x16 image. Black pixels represent 1 bits and white pixels represent 0 bits. For horizontal arrangements, the most significant bit is on the left as usual. For vertical arrangements, the most significant bit is on top.
Examples: The 8-bit number 15 (hexadecimal 0x0F, binary 0b00001111) is located horizontally at 3,4, which means X=3, Y=4.
- The pixel at 3,4 is white, which has bit value 0.
- 4,4 is white, also 0.
- 5,4 is white, also 0.
- 6,4 is white, also 0.
- 7,4 is black, which has bit value 1.
- 8,4, 9,4, and 10,4 are black, giving three more 1s.
- Reading them all off, this is 0b00001111, or 15.
15 is also located horizontally at 7,6.
The 8-bit number 0 is located vertically at 0,0. It is also located horizontally at 0,0 and 1,0.
The 8-bit number 134 (hexadecimal 0x86, binary 0b10000110) is located vertically at 8,4.
QUESTION DATAREP-3A. Where is 3 located vertically? (All questions refer to 8-bit numbers.)
QUESTION DATAREP-3B. Where is 12 located horizontally?
QUESTION DATAREP-3C. Where is 255 located vertically?
DATAREP-4. Hello memory
Shintaro Tsuji wants to represent the image of Question DATAREP-3 in computer memory. He stores it in an array of 16-bit unsigned integers:
unsigned short cute[16];
Row Y of the image is stored in integer cute[Y].
QUESTION DATAREP-4A. What is sizeof(cute), 2, 16, 32, or 64?
QUESTION DATAREP-4B. printf("%d\n", cute[0]); prints 16384. Is
Shintaro’s machine big-endian or little-endian?
DATAREP-5. Hello program
Now that Shintaro has represented the image in memory as an array of unsigned short objects, he can manipulate the image using C. For example, here’s a
function.
void swap(void) {
for (int i = 0; i < 16; ++i) {
cute[i] = (cute[i] << 8) | (cute[i] >> 8);
}
}
Running swap produces the following image:
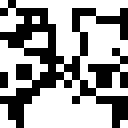
Shintaro has written several other functions. Here are some images (A is the original):
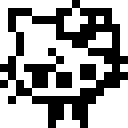 |
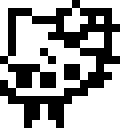 |
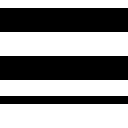 |
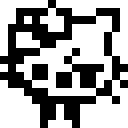 |
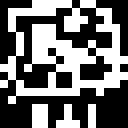 |
A |
B |
C |
D |
E |
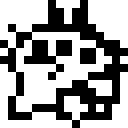 |
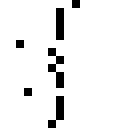 |
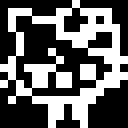 |
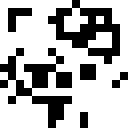 |
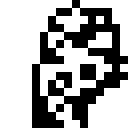 |
F |
G |
H |
I |
J |
For each function, what image does that function create?
QUESTION DATAREP-5A.
void f0() {
for (int i = 0; i < 16; ++i) {
cute[i] = ~cute[i];
}
}
QUESTION DATAREP-5B.
void f1() {
for (int i = 0; i < 16; ++i) {
cute[i] = ((cute[i] >> 1) & 0x5555) | ((cute[i] << 1) & 0xAAAA);
cute[i] = ((cute[i] >> 2) & 0x3333) | ((cute[i] << 2) & 0xCCCC);
cute[i] = ((cute[i] >> 4) & 0x0F0F) | ((cute[i] << 4) & 0xF0F0);
cute[i] = (cute[i] >> 8) | (cute[i] << 8);
}
}
QUESTION DATAREP-5C.
void f2() {
char* x = (char*) cute;
for (int i = 0; i < 16; ++i) {
x[2*i] = i;
}
}
For “fun”
The following programs generated the other images. Can you match them with their images?
void f3() {
for (int i = 0; i < 16; ++i) {
cute[i] &= ~(7 << i);
}
}
void f4() {
swap();
for (int i = 0; i < 16; ++i) {
cute[i] <<= i/4;
}
swap();
}
void f5() {
for (int i = 0; i < 16; ++i) {
cute[i] = -1 * !!(cute[i] & 64);
}
}
void f6() {
for (int i = 0; i < 8; ++i) {
int tmp = cute[15-i];
cute[15-i] = cute[i];
cute[i] = tmp;
}
}
void f7() {
for (int i = 0; i < 16; ++i) {
cute[i] = cute[i] & -cute[i];
}
}
void f8() {
for (int i = 0; i < 16; ++i) {
cute[i] ^= cute[i] ^ cute[i];
}
}
void f9() {
for (int i = 0; i < 16; ++i) {
cute[i] = cute[i] ^ 4080;
}
}
DATAREP-6. Memory regions
Consider the following program:
struct ptrs {
int** x;
int* y;
};
struct ptrs global;
void setup(struct ptrs* p) {
int* a = malloc(sizeof(int));
int* b = malloc(sizeof(int));
int* c = malloc(sizeof(int));
int* d = malloc(sizeof(int));
int* e = malloc(sizeof(int) * 2);
int** f = malloc(4 * sizeof(int*));
int** g = malloc(sizeof(int*));
*a = 0;
*b = 0;
*c = (int) a;
*d = *b;
e[0] = 29;
e[1] = (int) &d[100000];
f[0] = b;
f[1] = c;
f[2] = 0;
f[3] = 0;
*g = c;
global.x = f;
global.y = e;
p->x = g;
p->y = &e[1];
}
int main(int argc, char** argv) {
stack_bottom = (char*) &argc;
struct ptrs p;
setup(&p);
m61_collect(); // see next problem
do_stuff(&p);
}
This program allocates objects a through g on the heap and then stores
those pointers in some stack and global variables. We recommend you draw a
picture of the state setup creates.
QUESTION DATAREP-6A. Assume that (uintptr_t) a == 0x8300000, and
that malloc returns increasing addresses. Match each address to the
most likely expression with that address value. The expressions are
evaluated within the context of main. You will not reuse an
expression.
| Value | Expression | |||
|---|---|---|---|---|
| 1. | 0x8300040 | A. | &p |
|
| 2. | 0x8049894 | B. | (int*) *p.x[0] |
|
| 3. | 0x8361AF0 | C. | &global.y |
|
| 4. | 0x8300000 | D. | global.y |
|
| 5. | 0xBFAE0CD8 | E. | (int*) *p.y |
DATAREP-7. ⚠️ Garbage collection ⚠️
⚠️ Here is the top-level function for the conservative garbage collector we wrote in class.
void m61_collect(void) {
char* stack_top = (char*) &stack_top;
// The entire contents of the heap start out unmarked
for (size_t i = 0; i != nmr; ++i) {
mr[i].marked = 0;
}
// Mark all reachable objects, starting with the roots (the stack)
m61_markaccessible(stack_top, stack_bottom - stack_top);
// Free everything that wasn't marked
for (size_t i = 0; i != nmr; ++i) {
if (mr[i].marked == 0) {
m61_free(mr[i].ptr);
--i; // m61_free moved different data into this
// slot, so we must recheck the slot
}
}
}
This garbage collector is not correct because it doesn’t capture all memory roots.
Consider the program from the previous section, and assume that an
object is reachable if do_stuff can access an address within the
object via variable references and memory dereferences without casts or
pointer arithmetic. Then:
QUESTION DATAREP-7A. Which reachable objects will m61_collect()
free? List all that apply.
|--|-----|--|-----|--|-----|--|-----|--|-----|--|-----|--|-----|--|---------------|
| | a | | b | | c | | d | | e | | f | | g | | None of these |
QUESTION DATAREP-7B. Which unreachable objects will
m61_collect() not free? List all that apply.
|--|-----|--|-----|--|-----|--|-----|--|-----|--|-----|--|-----|--|---------------|
| | a | | b | | c | | d | | e | | f | | g | | None of these |
QUESTION DATAREP-7C. Conservative garbage collection in C is often slower than precise garbage collection in languages such as Java. Why? List all that apply.
- C is generally slower than other languages.
- Conservative garbage collectors must search all reachable memory for pointers. Precise garbage collectors can ignore values that do not contain pointers, such as large character buffers.
- C programs generally use the heap more than programs in other languages.
- None of the above.
DATAREP-8. Memory errors
The following function constructs and returns a lower-triangular matrix of size N. The elements are random 2-dimensional points in the unit square. The matrix is represented as an array of pointers to arrays.
struct point2 {
double d[2];
};
typedef point2* point2_vector;
point2_vector* make_random_lt_matrix(size_t N) {
point2_vector* m = (point2_vector*) malloc(sizeof(point2_vector) * N);
for (size_t i = 0; i < N; ++i) {
m[i] = (point2*) malloc(sizeof(point2) * (i + 1)); /* LINE A */
for (size_t j = 0; j <= i; ++j) {
for (int d = 0; d < 2; ++d) {
m[i][j].d[d] = drand48(); /* LINE B */
}
}
}
return m;
}
This code is running on an x86-32 machine (size_t is 32 bits,
not 64). You may assume that the machine has enough free physical memory
and the process has enough available virtual address space to satisfy
any memory allocation request.
QUESTION DATAREP-8A. Give a value of N so that, while
make_random_lt_matrix(N) is running, no new fails, but
a memory error (such as a null pointer dereference or an out-of-bounds
dereference) happens on Line A. The memory error should happen
specifically when i == 1.
(This problem is probably easier when you write your answer in hexadecimal.)
QUESTION DATAREP-8B. Give a value of N so that no new
fails, and no memory error happens on Line A, but a memory
error does happen on Line B.
DATAREP-9. Data representation
Assume a 64-bit x86-64 architecture unless explicitly told otherwise.
Write your assumptions if a problem seems unclear, and write down your reasoning for partial credit.
QUESTION DATAREP-9A. Arrange the following values in increasing
numeric order. Assume that x is an int with value 8192.
| a. | EOF |
e. | 1000 |
|
| b. | x & ~x |
f. | (signed char) 65535 |
|
| c. | (signed char) 0x47F |
g. | The size of the stdio cache | |
| d. | x | ~x |
h. | -0x80000000 |
A possible answer might be “a < b < c = d < e < f < g < h.”
For each of the remaining questions, write one or more arguments that, when passed to the provided function, will cause it to return the integer 61 (which is 0x3d hexadecimal). Write the expected number of arguments of the expected types.
QUESTION DATAREP-9B.
int f1(int n) {
return 0x11 ^ n;
}
QUESTION DATAREP-9C.
int f2(const char* s) {
return strtol(s, nullptr, 0);
}
QUESTION DATAREP-9D. Your answer should be different from the previous answer.
int f3(const char* s) {
return strtol(s, nullptr, 0);
}
QUESTION DATAREP-9E. For this problem, you will also need to define a global variable. Give its type and value.
f4:
andl $5, %edi
leal (%rsi,%rdi,2), %eax
movzbl y(%rip), %ecx
subl %ecx, %eax
retq
DATAREP-10. Sizes and alignments
Assume a 64-bit x86-64 architecture unless explicitly told otherwise.
Write your assumptions if a problem seems unclear, and write down your reasoning for partial credit.
QUESTION DATAREP-10A. Use the following members to create a struct
of size 16, using each member exactly once, and putting char a first;
or say “impossible” if this is impossible.
char a;(we’ve written this for you)unsigned char b;short c;int d;
struct size_16 {
char a;
};
QUESTION DATAREP-10B. Repeat Part A, but create a struct with size 12.
struct size_12 {
char a;
};
QUESTION DATAREP-10C. Repeat Part A, but create a struct with size 8.
struct size_8 {
char a;
};
QUESTION DATAREP-10D. Consider the following structs:
struct x {
T x1;
U x2;
};
struct y {
struct x y1;
V y2;
};
Give definitions for T, U, and V so that there is one byte of padding in
struct x after x2, and two bytes of padding in struct y after
y1.
DATAREP-11. Dynamic memory allocation
QUESTION DATAREP-11A. True or false?
free(nullptr)is an error.malloc(0)can never returnnullptr.
QUESTION DATAREP-11B. Give values for sz and nmemb so that calloc(sz, nmemb) will always return nullptr (on a 64-bit x86-64 machine), but
malloc(sz * nmemb) might or might not return null.
For parts C–F, consider the following 8 statements. (p and q
have type char* and start out as uninitialized variables.)
free(p);free(q);p = q;q = nullptr;p = (char*) malloc(12);q = (char*) malloc(8);p[8] = 0;q[4] = 0;
This tool will check your answers for parts C–F, but you should work out an answer to your satisfaction before checking it.
QUESTION DATAREP-11C. Put the statements in an order that would execute without error or evoking undefined behavior. Memory leaks count as errors. Use each statement exactly once. Sample answer: “abcdefgh.”
QUESTION DATAREP-11D. Put the statements in an order that would cause one double-free error, and no other error or undefined behavior (except possibly one memory leak). Use each statement exactly once.
QUESTION DATAREP-11E. Put the statements in an order that would cause one memory leak (one allocated piece of memory is not freed), and no other error or undefined behavior. Use each statement exactly once.
QUESTION DATAREP-11F. Put the statements in an order that would cause one boundary write error, and no other error or undefined behavior. Use each statement exactly once.
DATAREP-12. Pointers and debugging allocators
You are debugging some students’ m61 code from Problem Set 1. The
codes use the following metadata:
struct meta { ...
meta* next;
meta* prev;
};
meta* mhead; // head of active allocations list
Their linked-list manipulations in m61_malloc are similar.
void* m61_malloc(size_t sz, const char* file, int line) {
...
meta* m = (meta*) ptr;
m->next = mhead;
m->prev = nullptr;
if (mhead) {
mhead->prev = m;
}
mhead = m;
...
}
But their linked-list manipulations in m61_free differ.
Alice’s code:
void m61_free(void* ptr, ...) { ... meta* m = (meta*) ptr - 1; if (m->next != nullptr) { m->next->prev = m->prev; } if (m->prev == nullptr) { mhead = nullptr; } else { m->prev->next = m->next; } ... }
Bob’s code:
void m61_free(void* ptr, ...) { ... meta* m = (meta*) ptr - 1; if (m->next) { m->next->prev = m->prev; } if (m->prev) { m->prev->next = m->next; } ... }
Chris’s code:
void m61_free(void* ptr, ...) { ... meta* m = (meta*) ptr - 1; m->next->prev = m->prev; m->prev->next = m->next; ... }
Donna’s code:
void m61_free(void* ptr, ...) { ... meta* m = (meta*) ptr - 1; if (m->next) { m->next->prev = m->prev; } if (m->prev) { m->prev->next = m->next; } else { mhead = m->next; } ... }
You may assume that all code not shown is correct.
QUESTION DATAREP-12A. Whose code will segmentation fault (crash) on this input? List all students that apply.
int main() {
void* ptr = malloc(1);
free(ptr);
}
QUESTION DATAREP-12B. Whose code might report something like
“invalid free of pointer [ptr1], not allocated” on this input
(because a list traversal starting from mhead fails to find ptr1)?
List all students that apply. Don’t include students whose code would
crash before the report.
int main() {
void* ptr1 = malloc(1);
void* ptr2 = malloc(1);
free(ptr2);
free(ptr1); // <- message printed here
}
QUESTION DATAREP-12C. Whose code could improperly report a leaked piece of
memory on this input, or cause a crash in m61_printleakreport (because the
mhead list contains garbage)? List all students that apply. Don’t include
students whose code would segfault before the report.
int main() {
void* ptr1 = malloc(1);
free(ptr1);
m61_printleakreport();
}
QUESTION DATAREP-12D. Whose linked-list code is correct for all inputs? List all that apply.
DATAREP-13. Arena allocation
Chimamanda Ngozi Adichie is a writing a program that needs to allocate and free a lot of nodes, where a node is defined as follows:
struct node {
int key;
void* value;
node* left;
node* right; // also used in free list
};
She uses an arena allocator variant. Here’s her code.
struct arena_group {
arena_group* next_group;
node nodes[1024];
};
struct arena {
node* frees;
arena_group* groups;
};
node* node_alloc(arena* a) {
if (!a->frees) {
arena_group* g = new arena_group;
// ... link `g` to `a->groups` ...
for (size_t i = 0; i != 1023; ++i) {
g->nodes[i].right = &g->nodes[i + 1];
}
g->nodes[1023].right = nullptr;
a->frees = &g->nodes[0];
}
node* n = a->frees;
a->frees = n->right;
return n;
}
void node_free(arena* a, node* n) {
n->right = a->frees;
a->frees = n;
}
QUESTION DATAREP-13A. True or false?
- This allocator never has external fragmentation.
- This allocator never has internal fragmentation.
QUESTION DATAREP-13B. Chimamanda’s frenemy Paul Auster notices that if many nodes are allocated right in a row, every 1024th allocation seems much more expensive than the others. The reason is that every 1024th allocation initializes a new group, which in turn adds 1024 nodes to the free list. Chimamanda decides instead to allow a single element of the free list to represent many contiguous free nodes. The average allocation might get a tiny bit slower, but no allocation will be much slower than average. Here’s the start of her idea:
node* node_alloc(arena* a) {
if (!a->frees) {
arena_group* g = new arena_group;
// ... link `g` to `a->groups` ...
g->nodes[0].key = 1024; // g->nodes[0] is the 1st of 1024 contiguous free nodes
g->nodes[0].right = nullptr;
a->frees = &g->nodes[0];
}
node* n = a->frees;
// ???
return n;
}
Complete this function by writing code to replace // ???.
QUESTION DATAREP-13C. Write a node_free function that works with
the node_alloc function from the previous question.
void node_free(arena* a, node* n) {
}
QUESTION DATAREP-13D. Complete the following new function.
// Return the arena_group containing node `n`. `n` must be a node returned by
// a previous call to `node_alloc(a)`.
arena_group* node_find_group(arena* a, node* n) {
for (arena_group* g = a->groups; g; g = g->next_group) {
}
return nullptr;
}
QUESTION DATAREP-13E. Chimamanda doesn’t like that the
node_find_group function from part D takes O(G) time,
where G is the number of allocated arena_groups. She remembers a
library function that might help, posix_memalign:
int posix_memalign(void** memptr, size_t alignment, size_t size);
The function posix_memalign() allocates size bytes and places the
address of the allocated memory in *memptr. The address of the
allocated memory will be a multiple of alignment, which must be a
power of two and a multiple of sizeof(void*). ...
“Cool,” she says, “I can use this to speed up node_find_group!” She
now allocates a new group with the following code:
arena_group* g;
int r = posix_memalign(&g, 32768, sizeof(arena_group));
assert(r == 0); // posix_memalign succeeded
Given this allocation strategy, write a version of node_find_group
that takes O(1) time.
arena_group* node_find_group(arena* a, node* n) {
}
DATAREP-14. Data representation
Sort the following expressions in ascending order by value, using the operators <, =, >. For example, if we gave you:
int A = 6;int B = 0x6;int C = 3;
you would write C < A = B.
unsigned char a = 0x191;char b = 0x293;unsigned long c = 0xFFFFFFFF;int d = 0xFFFFFFFF;int e = d + 3;- f = 4 GB
size_t g = sizeof(*s)(givenshort *s)long h = 256;- i =
0b100000000000000000000000000000000000(binary) unsigned long j = 0xACE - 0x101;
DATAREP-15. Memory
For the following questions, select the part(s) of memory from the list below that best describes where you will find the object.
- heap
- stack
- between the heap and the stack
- in a read-only data segment
- in a text segment starting at address 0x00400000
- in a read/write data segment
- in a register
Assume the following code, compiled without optimization.
#include <stdio.h>
#include <stdlib.h>
const long maxitems = 1000;
struct info {
char name[20];
unsigned int age;
short height;
} s = { "sushi", 1, 9 };
int main(int argc, char* argv[]) {
static long L = 0xbadf00d;
unsigned long u = 0x8badf00d;
int i, num = maxitems + 1;
struct info *sp;
printf("What did you do? %lx?\n", u);
while (num > maxitems || num < 10) {
printf("How much of it did you eat? ");
scanf(" %d", &num);
}
sp = (struct info *)malloc(num * sizeof(*sp));
for (i = 0; i < num; i++) {
sp[i] = s;
}
return 0xdeadbeef;
}
QUESTION DATAREP-15A. The value 0xdeadbeef, when we are returning from main.
QUESTION DATAREP-15B. The variable maxitems
QUESTION DATAREP-15C. The structure s
QUESTION DATAREP-15D. The structure at sp[9]
QUESTION DATAREP-15E. The variable u
QUESTION DATAREP-15F. main
QUESTION DATAREP-15G. printf
QUESTION DATAREP-15H. argc
QUESTION DATAREP-15I. The number the user enters
QUESTION DATAREP-15J. The variable L
DATAREP-16. Memory and pointers
⚠️ This question may benefit from Unit 4, kernel programming. ⚠️
If multiple processes are sharing data via mmap, they may have the file
mapped at different virtual addresses. In this case, pointers to the
same object will have different values in the different processes. One
way to store pointers in mmapped memory so that multiple processes can
access them consistently is using relative pointers. Rather than storing
a regular pointer, you store the offset from the beginning of the
mmapped region and add that to the address of the mapping to obtain a
real pointer. An alternative representation is called self-relative
pointers. In this case, you store the difference in address between the
current location (i.e., the location containing the pointer) and the
location to which you want to point. Neither representation addresses
pointers between the mmapped region and the rest of the address space;
you may assume such pointers do not exist.
QUESTION DATAREP-16A. State one advantage that relative pointers have over self-relative pointers.
QUESTION DATAREP-16B. State one advantage that self-relative pointers have over relative pointers.
For the following questions, assume the following setup:
char* region; /* Address of the beginning of the region. */
// The following are sample structures you might find in
// a linked list that you are storing in an mmaped region.
struct ll1 {
unsigned value;
TYPE1 r_next; /* Relative Pointer. */
};
struct ll2 {
unsigned value;
TYPE2 sr_next; /* Self-Relative Pointer. */
};
ll1 node1;
ll2 node2;
QUESTION DATAREP-16C. Propose a type for TYPE1 and give 1 sentence why you chose that type.
QUESTION DATAREP-16D. Write a C expression to generate a (properly
typed) pointer to the element referenced by the r_next field of ll1.
QUESTION DATAREP-16E. Propose a type for TYPE2 and give 1 sentence why you chose that type.
QUESTION DATAREP-16F. Write a C expression to generate a (properly
typed) pointer to the element referenced by the sr_next field of ll2.
DATAREP-17. Data representation: Allocation sizes
union my_union {
int f1[4];
long f2[2];
};
int main() {
void* p = malloc(sizeof(char*));
my_union u;
my_union* up = &u;
....
}
How much user-accessible space is allocated on the stack and/or the heap by each of the following statements? Assume x86-64.
QUESTION DATAREP-17A. union my_union { ... };
QUESTION DATAREP-17B. void* p = malloc(sizeof(char*));
QUESTION DATAREP-17C. my_union u;
QUESTION DATAREP-17D. my_union* up = &u;
DATAREP-18. Data representation: ENIAC
Professor Kohler has been developing Eddie’s NIfty Awesome Computer (ENIAC). When he built the C compiler for ENIAC, he assigned the following sizes and alignments to C’s fundamental data types. (Assume that every other fundamental type has the same size and alignment as one of these.)
| Type | sizeof |
alignof |
|
|---|---|---|---|
char |
1 | 1 | |
char* |
16 | 16 | Same for any pointer |
short |
4 | 4 | |
int |
8 | 8 | |
long |
16 | 16 | |
long long |
32 | 32 | |
float |
16 | 16 | |
double |
32 | 32 |
QUESTION DATAREP-18A. This set of sizes is valid: it obeys all the requirements set by C’s abstract machine. Give one different size assignment that would make the set as a whole invalid.
QUESTION DATAREP-18B. What alignment must the ENIAC malloc guarantee?
For the following two questions, assume the following struct on the ENIAC:
struct s {
char f1[7];
char *f2;
short f3;
int f4;
};
QUESTION DATAREP-18C. What is sizeof(struct s)?
QUESTION DATAREP-18D. What is alignof(struct s)?
The remaining questions refer to this structure definition:
// This include file defines a struct inner, but you do not know anything
// about that structure, just that it exists.
#include "inner.hh"
struct outer {
char f1[3];
inner f2;
short f3;
int f4;
};
Indicate for each statement whether the statement is always true, possibly true, or never true on the ENIAC.
QUESTION DATAREP-18E: sizeof(outer) > sizeof(inner)
(Always / Possibly / Never)
QUESTION DATAREP-18F: sizeof(outer) is a multiple of
sizeof(inner) (Always / Possibly / Never)
QUESTION DATAREP-18G: alignof(outer) > alignof(struct inner) (Always / Possibly / Never)
QUESTION DATAREP-18H: sizeof(outer) - sizeof(inner) < 4 (Always / Possibly / Never)
QUESTION DATAREP-18I: sizeof(outer) - sizeof(inner) > 32 (Always / Possibly / Never)
QUESTION DATAREP-18J: alignof(inner) == 2
(Always / Possibly / Never)
DATAREP-19. Undefined behavior
Which of the following expressions, instruction sequences, and code
behaviors cause undefined behavior? For each question, write Defined or
Undefined. (Note that the INT_MAX and UINT_MAX constants have
types int and unsigned, respectively.)
QUESTION DATAREP-19A. INT_MAX + 1 (Defined / Undefined)
QUESTION DATAREP-19B. UINT_MAX + 1 (Defined / Undefined)
QUESTION DATAREP-19C.
movq $0x7FFFFFFFFFFFFFFF, %rax
addl $1, %rax
(Defined / Undefined)
QUESTION DATAREP-19D. Failed memory allocation, i.e., malloc
returns nullptr (Defined / Undefined)
QUESTION DATAREP-19E. Use-after-free (Defined / Undefined)
QUESTION DATAREP-19F. Here are two functions and a global variable:
const char string[128] = ".......";
int read_nth_char(int n) {
return string[n];
}
int f(int i) {
if (i & 0x40) {
return read_nth_char(i * 2);
} else {
return i * 2;
}
}
C’s undefined behavior rules would allow an aggressive optimizing
compiler to simplify the code generated for f. Fill in the following
function with the simplest C code you can, under the constraint that an
aggressive optimizing compiler might generate the same object code for
f and f_simplified.
int f_simplified(int i) {
}
DATAREP-20. Bit manipulation
It’s common in systems code to need to switch data between big-endian and little-endian representations. This is because networks represent multi-byte integers using big-endian representation, whereas x86-family processors store multi-byte integers using little-endian representation.
QUESTION DATAREP-20A. Complete this function, which translates an integer
from big-endian representation to little-endian representation by swapping
bytes. For instance, big_to_little(0x01020304) should return 0x04030201.
Your return statement must refer to the u.c array, and must not
refer to x. This function is compiled on x86-64 Linux (as every function is
unless we say otherwise).
unsigned big_to_little(unsigned x) {
union {
unsigned intval;
unsigned char c[4];
} u;
u.intval = x;
return ______________________________________;
}
QUESTION DATAREP-20B. Complete the function again, but this time
write a single expression that refers to x (you may refer to x
multiple times, of course).
unsigned big_to_little(unsigned x) {
return ______________________________________;
}
QUESTION DATAREP-20C. Now write the function little_to_big,
which will translate a little-endian integer into big-endian
representation. You may introduce helper variables or even call
big_to_little if that’s helpful.
unsigned little_to_big(unsigned x) {
}
DATAREP-21. Computer arithmetic
Bitwise operators and computer arithmetic can represent vectors of
bits, which in turn are useful for representing sets. For example, say
we have a function bit that maps elements to distinct bits; thus,
bit(X) == (1 << i) for some i. Then a set {X0, X1, X2, …, Xn} can be
represented as bit(X0) | bit(X1) | bit(X2) | … | bit(Xn). Element Xi
is in the set with integer representation z if and only if (bit(Xi) & z) != 0.
QUESTION DATAREP-21A. What is the maximum number of set elements
that can be represented in a single unsigned variable on an x86
machine?
QUESTION DATAREP-21B. Match each set operation with the C operator(s) that could implement that operation. (Complement is a unary operation.)
| intersection | == |
|
| equality | ~ |
|
| complement | & |
|
| union | ^ |
|
| toggle membership (flip whether an element is in the set) |
| |
QUESTION DATAREP-21C. Complete this function, which should return
the set difference between the sets with representations a and b.
This is the set containing exactly those elements of set a that are
not in set b.
unsigned set_difference(unsigned a, unsigned b) {
}
QUESTION DATAREP-21D. Below we’ve given a number of C++ expressions,
some of their values, and some of their set representations for a set of
elements. For example, the first row says that the integer value of
expression 0 is just 0, which corresponds to an empty set. Fill in the
blanks. This will require figuring out which bits correspond to the set
elements A, B, C, and D, and the values for the 32-bit int
variables a, x, and s. No arithmetic operation overflows; abs(x)
returns the absolute value of x (that is, x < 0 ? -x : x).
Expression e |
Integer value | Represented set |
|---|---|---|
0 |
0 | {} |
a == a |
______________ | {A} |
(unsigned) ~a < (unsigned) a |
______________ | {A} |
a < 0 |
______________ | ______________ |
(1 << (s/2)) - 1 |
______________ | {A,B,C,D} |
a * a |
______________ | {C} |
abs(a) |
______________ | ______________ |
x & (x - 1) |
______________ | {} |
x - 1 |
______________ | {A,D} |
x |
______________ | ______________ |
s |
______________ | ______________ |
DATAREP-22. Bit Tac Toe
Brenda Bitdiddle is implementing tic-tac-toe using bitwise arithmetic. (If you’re unfamiliar with tic-tac-toe, see below.) Her implementation starts like this:
struct tictactoe {
unsigned moves[2];
};
#define XS 0
#define OS 1
void tictactoe_init(tictactoe* b) {
b->moves[XS] = b->moves[OS] = 0;
}
static const unsigned ttt_values[3][3] = {
{ 0x001, 0x002, 0x004 },
{ 0x010, 0x020, 0x040 },
{ 0x100, 0x200, 0x400 }
};
// Mark a move by player `p` at row `row` and column `col`.
// Return 0 on success; return –1 if position `row,col` has already been used.
int tictactoe_move(tictactoe* b, int p, int row, int col) {
1. assert(row >= 0 && row < 3 && col >= 0 && col < 3);
2. assert(p == XS || p == OS);
3. /* TODO: check for position reuse */
4. b->moves[p] |= ttt_values[row][col];
5. return 0;
}
Each position on the board is assigned a distinct bit.
Tic-tac-toe, also known as noughts and crosses, is a simple paper-and-pencil game for two players, X and O. The board is a 3x3 grid. The players take turns writing their symbol (X or O) in an empty square on the grid. The game is won when one player gets their symbol in all three squares in one of the rows, one of the columns, or one of the two diagonals. X goes first; played perfectly, the game always ends in a draw.
You may access the Wikipedia page for tic-tac-toe.
QUESTION DATAREP-22A. Brenda’s current code doesn’t check whether a move reuses a position. Write a snippet of C code that returns –1 if an attempted move is reusing a position. This snippet will replace line 3.
QUESTION DATAREP-22B. Complete the following function. You may use the following helper function:
int popcount(unsigned n)
Return the number of 1 bits inn. (Stands for “population count”; is implemented on recent x86 processors by a single instruction,popcnt.)
For full credit, your code should consist of a single “return”
statement with a simple expression, but for substantial partial credit
write any correct solution.
// Return the number of moves that have happened so far.
int tictactoe_nmoves(const tictactoe* b) {
}
QUESTION DATAREP-22C. Write a simple expression that, if nonzero,
indicates that player XS has a win on board b across the main
diagonal (has marks in positions 0,0, 1,1, and 2,2).
Lydia Davis notices Brenda’s code and has a brainstorm. “If you use different values,” she suggests, “it becomes easy to detect any win.” She suggests:
static const unsigned ttt_values[3][3] = {
{ 0x01001001, 0x00010002, 0x10100004 },
{ 0x00002010, 0x22020020, 0x00200040 },
{ 0x40004100, 0x00040200, 0x04400400 }
};
QUESTION DATAREP-22D. Repeat part A for Lydia’s values: Write a snippet of C code that returns –1 if an attempted move is reusing a position. This snippet will replace line 3 in Brenda’s code.
QUESTION DATAREP-22E. Repeat part B for Lydia’s values: Use
popcount to complete tictactoe_nmoves.
int tictactoe_nmoves(const tictactoe* b) {
}
QUESTION DATAREP-22F. Complete the following function for Lydia’s
values. For full credit, your code should consist of a single “return”
statement containing exactly two constants, but for substantial partial
credit write any correct solution.
// Return nonzero if player `p` has won, 0 if `p` has not won.
int tictactoe_check_win(const tictactoe* b, int p) {
assert(p == XS || p == OS);
}
DATAREP-23. Memory and Pointers
Two processes are mapping a file into their address space. The mapped file contains an unsorted linked list of integers. As the processes cannot ensure that the file will be mapped at the same virtual address, they use relative pointers to link elements in the list. A relative pointer holds not an address, but an offset that user code can use to calculate a true address. Our processes define the offset as relative to the start of the file.
Thus, each element in the linked list is represented by the following structure:
struct ll_node {
int value;
size_t offset;
};
offset == (size_t) -1 indicates the end of the list. Other
offset values represent the position of the next item in the list,
calculated relative to the start of the file.
QUESTION DATAREP-23A. Write a function to find an item in the list. The function's prototype is:
ll_node* find_element(void* mapped_file, ll_node* list, int value);
The mapped_file parameter is the address of the mapped file data;
the list parameter is a pointer to the first node in the list; and
the value parameter is the value for which we are searching. The
function should return a pointer to the linked list element if the value
appears in the list or nullptr if the value is not in the list.
DATAREP-24. Integer representation
Write the value of the variable or expression in each problem, using signed decimal representation.
For example, if we gave you:
int i = 0xA;int j = 0xFFFFFFFF;
you would write A) 10 B) -1.
QUESTION DATAREP-24A. int i = 0xFFFF; (You may write this either
in decimal or as an expression using a power of 2)
QUESTION DATAREP-24B. short s = 0xFFFF; (You may write this
either in decimal or as an expression using a power of 2)
QUESTION DATAREP-24C. unsigned u = 1 << 10;
QUESTION DATAREP-24D. ⚠️ From WeensyOS: unsigned long l = PTE_P | PTE_U;
QUESTION DATAREP-24E. int j = ~0;
QUESTION DATAREP-24F. ⚠️ From WeensyOS: sizeof(x86_64_pagetable);
QUESTION DATAREP-24G. Given this structure:
struct s {
char c;
short s;
long l;
};
s* ps;
This expression: sizeof(ps);
QUESTION DATAREP-24H. Using the structure above: sizeof(*ps);
QUESTION DATAREP-24I. unsigned char u = 0xABC;
QUESTION DATAREP-24J. signed char c = 0xABC;
DATAREP-25. Data representation
In gdb, you observe the following values for a set of memory locations.
0x100001020: 0xa0 0xb1 0xc2 0xd3 0xe4 0xf5 0x06 0x17
0x100001028: 0x28 0x39 0x4a 0x5b 0x6c 0x7d 0x8e 0x9f
0x100001030: 0x89 0x7a 0x6b 0x5c 0x4d 0x3e 0x2f 0x10
0x100001038: 0x01 0xf2 0xe3 0xd4 0xc5 0xb6 0xa7 0x96
For each C expression below, write its value in hexadecimal. For example, if we gave you:
char *cp = (char*) 0x100001020; cp[0] =
the answer would be 0xa0.
Assume the following structure and union declarations and variable definitions.
struct _s1 {
int i;
long l;
short s;
};
struct _s2 {
char c[4];
int i;
struct _s1 s;
};
union _u {
char c[8];
int i;
long l;
short s;
};
char* cp = (char*) 0x100001020;
struct _s1* s1 = (struct _s1*) 0x100001020;
struct _s2* s2 = (struct _s2*) 0x100001020;
union _u* u = (union _u*) 0x100001020;
QUESTION DATAREP-25A. cp[4] =
QUESTION DATAREP-25B. cp + 7 =
QUESTION DATAREP-25C. s1 + 1 =
QUESTION DATAREP-25D. s1->i =
QUESTION DATAREP-25E. sizeof(s1) =
QUESTION DATAREP-25F. &s2->s =
QUESTION DATAREP-25G. &u->s =
QUESTION DATAREP-25H. s1->l =
QUESTION DATAREP-25I. s2->s.s =
QUESTION DATAREP-25J. u->l =
DATAREP-26. Sizes and alignments
Here’s a test struct with n members. Assume an x86-64 machine, where
each Ti either is a basic x86-64 type (e.g., int, char,
double) or is a type derived from such types (e.g., arrays, structs,
pointers, unions, possibly recursively), and assume that ai≤8 for all
i.
struct test {
T1 m1; // sizeof(T1) == s1, alignof(T1) == a1
T2 m2; // sizeof(T2) == s2, alignof(T2) == a2
...
Tn mn; // sizeof(Tn) == sn, alignof(Tn) == an
};
In these questions, you will compare this struct with other structs that have the same members, but in other orders.
QUESTION DATAREP-26A. True or false: The size of struct test is minimized
when its members are sorted by size. In other words, if
s1≤s2≤…≤sn, then sizeof(struct test) is less than or
equal to the struct size for any other member order.
If true, briefly explain your answer; if false, give a counterexample
(i.e., concrete types for T1, …, Tn that do not minimize
sizeof(struct test)).
QUESTION DATAREP-26B. True or false: The size of struct test is minimized
when its members are sorted by alignment. In other words, if
a1≤a2≤…≤an, then sizeof(struct test) is less than or
equal to the struct size for any other member order.
If true, briefly explain your answer; if false, give a counterexample.
QUESTION DATAREP-26C. True or false: The alignment of struct test is
minimized when its members are sorted in increasing order by alignment.
In other words, if a1≤a2≤…≤an, then
alignof(struct test) is less than or equal to the struct
alignment for any other member order.
If true, briefly explain your answer; if false, give a counterexample.
QUESTION DATAREP-26D. What is the maximum number of bytes of padding that
struct test could contain for a given n? The answer will be a pretty
simple formula involving n. (Remember that ai≤8 for all i.)
QUESTION DATAREP-26E. What is the minimum number of bytes of padding that
struct test could contain for a given n?
DATAREP-27. Undefined behavior
QUESTION DATAREP-27A. Sometimes a conforming C compiler can assume that a + 1 > a, and sometimes it can’t. For each type below, consider this
expression:
a + (int) 1 > a
and say whether the compiler:
- Must reject the expression as a type error.
- May assume that the expression is true (that
a + (int) 1 > afor alla). - Must not assume that the expression is true.
int aunsigned achar* aunsigned char astruct {int m;} a
QUESTION DATAREP-27B. The following code checks its arguments for sanity, but not well: each check can cause undefined behavior.
void sanity_check(int* array, size_t array_size, int* ptr_into_array) {
if (array + array_size < array) {
fprintf(stderr, "`array` is so big that it wraps around!\n");
abort();
}
if (ptr_into_array < array || ptr_into_array > array + array_size) {
fprintf(stderr, "`ptr_into_array` doesn’t point into the array!\n");
abort();
}
...
Rewrite these checks to avoid all undefined behavior. You will likely
add one or more casts to uintptr_t. For full credit, write each
check as a single comparison (no && or ||, even though the current
ptr_into_array check uses ||).
array_size check:
ptr_into_array check:
QUESTION DATAREP-27C. In lecture, we discussed several ways to tell
if a signed integer x is negative. One of them was the following:
int isnegative = (x & (1UL << (sizeof(x) * CHAR_BIT))) != 0;
But this is incorrect: it has undefined behavior. Correct it by adding two characters.
DATAREP-28. ⚠️ Memory errors and garbage collection ⚠️
⚠️ We didn’t discuss garbage collectors in class this year.
Recall that a conservative garbage collector is a program that can automatically free dynamically-allocated memory by detecting when that memory is no longer referenced. Such a GC works by scanning memory for currently-referenced pointers, starting from stack and global memory, and recursing over each referenced object until all referenced memory has been scanned. We built a conservative garbage collector in lecture datarep6.
QUESTION DATAREP-28A. An application program that uses conservative GC, and
does not call free directly, will avoid certain errors and undefined
behaviors. Which of the following errors are avoided? List all that
apply.
- Use-after-free
- Double free
- Signed integer overflow
- Boundary write error
- Unaligned access
QUESTION DATAREP-28B. Write a C program that leaks unbounded memory without GC, but does not do so with GC. You should need less than 5 lines. (Leaking “unbounded” memory means the program will exhaust the memory capacity of any machine on which it runs.)
QUESTION DATAREP-28C. Not every valid C program works with a conservative GC, because the C abstract machine allows a program to manipulate pointers in strange ways. Which of the following pointer manipulations might cause the conservative GC from class to inappropriately free a memory allocation? List all that apply.
-
Storing the pointer in a
uintptr_tvariable -
Writing the pointer to a disk file and reading it back later
-
Using the least-significant bit of the pointer to store a flag:
int* set_ptrflag(int* x, int flagval) { return (int*) ((uintptr_t) x | (flagval ? 1 : 0)); } int get_ptrflag(int* x) { return (uintptr_t) x & 1; } int deref_ptrflag(int* x) { return *((int*) ((uintptr_t) x & ~1UL)); } -
Storing the pointer in textual form:
void save_ptr(char buf[100], void* p) { sprintf(buf, "%p", p); } void* restore_ptr(const char buf[100]) { void* p; sscanf(buf, "%p", &p); return p; } -
Splitting the pointer into two parts and storing the parts in an array:
typedef union { unsigned long ival; unsigned arr[2]; } value; value save_ptr(void* p) { value v; v.arr[0] = (uintptr_t) p & 0xFFFFFFFFUL; v.arr[1] = ((uintptr_t) p / 4294967296UL) & 0xFFFFFFFFUL; return v; }
DATAREP-29. Bitwise
QUESTION DATAREP-29A. Consider this C fragment:
uintptr_t x = ...;
uintptr_t r = 0;
if (a < b) {
r = x;
}
Or, shorter:
uintptr_t r = a < b ? x : 0;
Write a single expression that evaluates to the same value, but that
does not use the conditional ?: operator. You will use the fact that
a < b always equals 0 or 1. For full credit, do not use expensive
operators (multiply, divide, modulus).
QUESTION DATAREP-29B. This function returns one more than the index of the least-significant 1 bit in its argument, or 0 if its argument is zero.
int ffs(unsigned long x) {
for (int i = 0; i < sizeof(x) * CHAR_BIT; ++i) {
if (x & (1UL << i)) {
return i + 1;
}
}
return 0;
}
This function runs in O(B) time, where B is the number of bits in
an unsigned long. Write a version of ffs that runs instead in
O(log B) time.
DATAREP-30. Data representation
QUESTION DATAREP-30A. Write a type whose size is 19,404,329 times larger than its alignment.
QUESTION DATAREP-30B. Consider a structure type T with N members, all
of which have nonzero size. Assume that sizeof(T) == alignof(T). What is N?
QUESTION DATAREP-30C. What is a C type that obeys (T) -1 == (T) 255 on
x86-64?
Parts D–G use this code. The architecture might or might not be x86-64.
unsigned char a[] = {
0x7A, 0xEC, 0x0D, 0xBE, 0x99, 0x0A, 0xD8, 0x0E
};
unsigned* s1 = (unsigned*) &a[0];
unsigned* s2 = s1 + 1;
Assume that (uintptr_t) s2 - (uintptr_t) s1 == 4 and *s1 > *s2.
QUESTION DATAREP-30D. What is sizeof(a)?
QUESTION DATAREP-30E. What is sizeof(unsigned) on this architecture?
QUESTION DATAREP-30F. Is this architecture big-endian or little-endian?
QUESTION DATAREP-30G. Might the architecture be x86-64?
DATAREP-31. Memory errors
Mavis Gallant is starting on her debugging memory allocator. She’s
written code that aims to detect invalid frees, where a pointer passed
to m61_free was not returned by an earlier
m61_malloc.
D1. struct m61_metadata {
D2. size_t magic;
D3. size_t padding;
D4. };
M1. void* m61_malloc(size_t sz) {
M2. m61_metadata* meta = base_malloc(sz + sizeof(m61_metadata));
M3. meta->magic = 0x84157893401;
M4. return (void*) (meta + 1);
M5. }
F1. void m61_free(void* ptr) {
F2. m61_metadata* meta = (m61_metadata*) ptr - 1;
F3. if (meta->magic != 0x84157893401) {
F4. fprintf(stderr, "invalid free of %p\n", ptr);
F5. abort();
F6. }
F7. base_free(meta);
F8. }
C1. void* m61_calloc(size_t count, size_t sz) {
C2. void* p = m61_malloc(sz * count);
C3. memset(p, 0, sz * count);
C4. return p;
C5. }`
Help her track down bugs.
QUESTION DATAREP-31A. What is sizeof(struct m61_metadata)?
QUESTION DATAREP-31B. Give an m61_ function call (function name and
arguments) that would cause both unsigned integer overflow and invalid
memory accesses.
QUESTION DATAREP-31C. Give an m61_ function call (function name and
arguments) that would cause integer overflow, but no invalid memory
access within the m61_ functions. (The application might or might
not make an invalid memory access later.)
QUESTION DATAREP-31D. These functions have some potential null pointer dereferences. Fix one such problem, including the line number(s) where your code should go.
QUESTION DATAREP-31E. Put a single line of C code in the blank. The
resulting program should (1) be well-defined with no memory leaks when
using default malloc/free/calloc, but (2) always cause
undefined behavior when using Mavis’s debugging
malloc/free/calloc.
... #includes ...
int main() {
________________________
}
QUESTION DATAREP-31F. A double free should print a different message than an invalid free. Write code so Mavis’s implementation does this; include the line numbers where the code should go.
DATAREP-32. Memory word search
QUESTION DATAREP-32A. What is decimal 61 in hexadecimal?
The following is a partial dump of an x86-64 Linux program’s memory. Note that each byte is represented as a hexadecimal number. Memory addresses increase from top to bottom and from left to right.
..0 ..1 ..2 ..3 ..4 ..5 ..6 ..7 ..8 ..9 ..a ..b ..c ..d ..e ..f
601080: 00 00 00 00 4f ef 38 1e 47 97 48 45 ff ff 00 00
601090: ff ff ff ff c3 ff ff ff 3d 00 00 00 30 c7 5f 14
6010a0: 3d 00 00 00 00 00 00 00 70 7e 1b 01 00 00 00 00
6010b0: 7c 2d 8f ba fd 7f 00 00 c3 ff ff ff ff ff ff ff
6010c0: a0 10 60 00 00 00 00 00 49 20 74 6f 6f 6b 20 36
6010d0: 31 00 00 00 00 00 00 00 47 9d ff ff ff 7f 00 00
QUESTION DATAREP-32B. What memory segment contains the memory dump?
For questions 3C–3I, give the last two digits of the address of the given object in this memory dump (so for the object located at address 0x6010a8, you would write “a8”). There’s a single best answer for every question, and all questions have different answers.
QUESTION DATAREP-32C. A long (64 bits) of value 61.
QUESTION DATAREP-32D. A long of value -61.
QUESTION DATAREP-32E. An int of value 61.
QUESTION DATAREP-32F. A pointer to an object in the heap.
QUESTION DATAREP-32G. A pointer to a local variable.
QUESTION DATAREP-32H. A pointer that points to an object present in the memory dump.
QUESTION DATAREP-32I. The first byte of a C string comprising at least 4 printable ASCII characters. (Printable ASCII characters have values from 0x20 to 0x7e.)
DATAREP-33. Architecture
QUESTION DATAREP-33A. Write a C++ expression that will evaluate to false on all typical 32-bit architectures and true on all typical 64-bit architectures.
QUESTION DATAREP-33B. Give an integer value that has the same representation in big-endian and little-endian, and give its C++ type. Assume the same type sizes as x86-64.
QUESTION DATAREP-33C. Repeat question B, but with a different integer value.
QUESTION DATAREP-33D. Complete this C++ function, which should return true iff it is called on a machine with little-endian integer representation. Again, you may assume the same type sizes as x86-64.
bool is_little_endian() {
}
DATAREP-34. Undefined behavior
The following code is taken from the well-known textbook Mastering C Pointers (with some stylistic changes). Assume it is run on x86-64.
#include <stdlib.h>
#include <stdio.h>
void main() {
int* x = malloc(400);
if (x == nullptr) {
printf("Out of memory\n");
exit(0);
} else {
for (int y = 0; y <= 198; ++x) {
*(x + y) = 88;
}
}
}
QUESTION DATAREP-34A. List all situations in which this program will not execute undefined behavior. (There is at least one.)
QUESTION DATAREP-34B. True or false? The expression ++x could be replaced with
++y without changing the meaning of the program.
Here’s an updated version of the program.
#include <stdlib.h>
#include <stdio.h>
void main() {
int* x = malloc(sizeof(int) * 200);
if (x == nullptr) {
printf("Out of memory\n");
exit(0);
} else {
for (int y = 0; y <= 198; ++y) {
*(x + y) = 88;
}
int i = random() % 200;
printf("x[%d] == %d\n", i, x[i]);
}
}
QUESTION DATAREP-34C. True or false? The expression *(x + y) could be replaced
with x[y] without changing the meaning of the program.
QUESTION DATAREP-34D. True or false? The expression *(x + y) could be replaced by * (int*) ((uintptr_t) x + y) without changing the meaning of the program.
DATAREP-35. Odd alignments
QUESTION DATAREP-35A. Write a struct definition that contains exactly seven bytes
of padding on x86-64.
QUESTION DATAREP-35B. Can an x86-64 struct comprise more than half padding? Give
an example if so, or explain briefly why not.
The remaining questions consider a new architecture called x86-64-rainbow, which is like x86-64 plus special support for a fundamental data type called color. A color is a three-byte data type with red, green, and blue components, kind of like this:
struct color {
unsigned char red;
unsigned char green;
unsigned char blue;
};
But unlike struct color on x86-64, which has size 3 and alignment 1,
color on x86-64-rainbow has size 3 and alignment 3. All the usual rules
for C abstract machine sizes and alignments still hold.
QUESTION DATAREP-35C. What is the alignment of pointers returned by malloc on
x86-64-rainbow?
QUESTION DATAREP-35D. Give an example of an x86-64-rainbow struct that ends with
more than 16 bytes of padding.
DATAREP-36. Debugging allocators
In problem set 1, you built a debugging allocator that could detect many kinds of error. Some students used exclusively internal metadata, where the debugging allocator’s data was stored within the same block of memory as the payload. Some students used external metadata, such as a separate hash table mapping payload pointers to metadata information.
QUESTION DATAREP-36A. Which kind of error mentioned by the problem set could not be detected by external metadata alone?
The problem set requires the m61 library to detect invalid frees, which includes double frees. However, double frees are so common that a special double-free error message can help users. Jia Tolentino wants to print such a message. Her initial idea is to keep a set of recently freed pointers:
static void* recently_freed[10];
static size_t recently_freed_index;
static bool is_recently_freed(void* ptr) {
for (int i = 0; i != 10; ++i) {
if (recently_freed[i] == ptr) {
return true;
}
}
return false;
}
static void add_recently_freed(void* ptr) {
recently_freed[recently_freed_index] = ptr;
recently_freed_index = (recently_freed_index + 1) % 10;
}
QUESTION DATAREP-36B. What eviction policy is used for the recently_freed array?
Jia uses these helpers in m61_free as follows. (You may assume that
is_invalid_free(ptr) returns true for every invalid or double
free.)
void m61_free(void* ptr, const char* file, int line) {
if (ptr != nullptr) {
if (is_recently_freed(ptr)) {
fprintf(stderr, "... double-free message ...");
abort();
} else if (is_invalid_free(ptr)) {
fprintf(stderr, "... invalid-free message ...");
abort();
} else {
add_recently_freed(ptr);
... actually free `ptr` ...
}
}
}
She has not yet changed m61_malloc, though she knows she needs to. Help her
evaluate whether her design achieves the following mandatory and desirable
(that is, optional) requirements.
Note: As you saw in tests 32 and 33 in pset 1, aggressive attacks from users can corrupt metadata arbitrarily. You should assume for the following questions that such aggressive attacks do not occur. The user might free something that was never allocated, and might double-free something, but will never overwrite metadata.
QUESTION DATAREP-36C. Mandatory: The design must not keep unbounded, un-reusable state for pointers that have been freed. Write “Achieved” or “Not achieved” and explain briefly.
QUESTION DATAREP-36D. Desirable: The design should report a double-free as a double-free, not an invalid free. Write “Achieved” or “Not achieved” and explain briefly.
QUESTION DATAREP-36E. Mandatory: The design must never report valid frees as double-frees or invalid frees. Write “Achieved” or “Not achieved” and explain briefly.
QUESTION DATAREP-36F. Describe code to be added to m61_malloc that will achieve
all mandatory requirements, if any are required.
DATAREP-37. Representations
Your job in the following questions is to complete each C++ program so that it
prints 61 to standard output when run. Your answer should fill in the blank
_________, and you may assume system calls execute without error. If a
question cannot be answered so that the program reliably prints 61 with no
undefined behavior, say so and explain briefly.
To compile these programs, use a command line such as c++ -std=gnu++17 -pthread x.cc.
QUESTION DATAREP-37A.
#include <cstdio>
int main() {
printf("%d\n", _________);
}
QUESTION DATAREP-37B.
#include <cstdio>
int main() {
printf("%ld\n", _________);
}
QUESTION DATAREP-37C.
#include <cstdio>
int main() {
printf("%x\n", _________);
}
QUESTION DATAREP-37D.
#include <cstdio>
int main() {
unsigned x = 4294967200;
printf("%d\n", x + _________);
}
QUESTION DATAREP-37E.
#include <cstdio>
struct sixtyfun {
_________
};
int main() {
printf("%zu\n", sizeof(sixtyfun));
}
QUESTION DATAREP-37F.
#include <cstdio>
struct sixtyfun {
int i;
_________
};
int main() {
printf("%zu\n", sizeof(sixtyfun));
}
QUESTION DATAREP-37G.
#include <cstdio>
#include <cstdint>
struct sixtyfun {
unsigned long larr[6];
_________
char carr[10];
};
int main() {
sixtyfun x;
printf("%zu\n", (uintptr_t) &x.carr[1] - (uintptr_t) &x.larr[1]);
}
QUESTION DATAREP-37H.
#include <cstdio>
#include <cassert>
int main() {
unsigned x = 419618010;
assert(x == 0x1902DCDA);
_________
printf("%d\n", ((x | a) >> b) & c);
}
QUESTION DATAREP-37I.
#include <cstdio>
int main() {
int x;
int y = x + 1;
printf("%d\n", y - x + _________);
}
QUESTION DATAREP-37J.
#include <cstdio>
#include <unistd.h>
int main() {
int x[10] = { 10, 11, 12, 13, 14, 15, 16, 17, 18, 19 };
for (int i = 0; i <= STDERR_FILENO; ++i) {
x[i] += _________;
}
printf("%d\n", x[0] + x[1] + x[2] + x[3]);
}
QUESTION DATAREP-37K.
#include <cstdio>
#include <cassert>
#include <unistd.h>
int main() {
const char* args[] = _________;
int r = execvp(args[0], (char**) args);
assert(r >= 0);
}
QUESTION DATAREP-37L.
#include <cstdio>
#include <cassert>
#include <unistd.h>
int main() {
int pfd[2];
int r = pipe(pfd);
assert(r >= 0);
pid_t p = fork();
assert(p >= 0);
if (p == 0) {
_________
const char* args[] = {"cat", nullptr};
r = execvp(args[0], (char**) args);
assert(r >= 0);
}
close(pfd[0]);
ssize_t nw = write(pfd[1], "61\n", 3);
assert(nw == 3);
close(pfd[1]);
sleep(3);
}
QUESTION DATAREP-37M.
#include <cstdio>
#include <cassert>
#include <unistd.h>
#include <sys/wait.h>
int main() {
pid_t p = fork();
assert(p >= 0);
if (p == 0) {
printf("6");
fflush(stdout);
_exit(0);
}
_________
printf("1\n");
}
QUESTION DATAREP-37N. Note that there are three blanks to fill in with code (you may also leave them empty).
#include <cstdio>
#include <thread>
#include <mutex>
#include <condition_variable>
#include <unistd.h>
int x;
std::mutex m;
std::condition_variable cv;
void tf(int low, int high) {
_________#1
if (low + 1 == high) {
_________#2
++x;
} else {
_________#3
int mid = low + (high - low) / 2;
std::thread t1(tf, low, mid);
std::thread t2(tf, mid, high);
t1.join();
t2.join();
}
}
int main() {
std::thread t(tf, 0, 61);
t.join();
printf("%d\n", x);
}
DATAREP-38. Memory layout
The following code computes a Fibonacci number.
#include <cerrno>
#include <getopt.h>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <unistd.h>
// copied from <cstdio> for your reference:
#define EOF (-1)
// copied from <getopt.h> for your reference:
extern int optind;
static void usage() {
fprintf(stderr, "Usage: ./fib NUMBER\n");
exit(1);
}
unsigned long fib(unsigned long n) {
if (n < 2) {
return n;
} else {
unsigned long tmp1 = fib(n - 1);
unsigned long tmp2 = fib(n - 2);
return tmp1 + tmp2;
}
}
int main(int argc, char *argv[]) {
// process command line options
char ch;
while ((ch = getopt(argc, argv, "h")) != EOF) {
switch (ch) {
case 'h':
case '?':
default:
usage();
}
}
// skip processed options
argc -= optind;
argv += optind;
// require 1 argument
if (argc != 1) {
usage();
}
// parse argument
unsigned long n = strtoul(strdup(argv[0]), nullptr, 10);
if (n == 0 && errno == EINVAL) {
usage();
}
// print fib(n)
unsigned long f = fib(n);
printf("fib(%lu) = %lu\n", n, f);
}
QUESTION DATAREP-38A. What are fib(0), fib(1), and fib(2)?
QUESTION DATAREP-38B. What are sizeof(fib(0)), sizeof(fib(1)), and sizeof(fib(2))?
For parts C–H, select from the list below the part of memory that best describes where you will find the object.
- In the heap
- In the stack
- Between the heap and the stack
- In a read-only data segment
- In a code segment
- In a read/write data segment
QUESTION DATAREP-38C. The string "fib(%lu) = %lu\n" (line 58).
QUESTION DATAREP-38D. optind (line 12)
QUESTION DATAREP-38E. tmp1 (line 23)
QUESTION DATAREP-38F. fib (lines 19-27)
QUESTION DATAREP-38G. strdup (line 51)
QUESTION DATAREP-38H. The string being passed to strtoul (line 51).
(Read the manual page for
strdup first!)
QUESTION DATAREP-38I. Does this program contain a memory leak?
QUESTION DATAREP-38J. Consider a call to fib(10) that was called from
fib(11). Will fib(10)’s tmp1 variable have a larger, smaller, or equal
address as fib(11)’s?
DATAREP-39. Basics
QUESTION DATAREP-39A. How many bits are in a long?
QUESTION DATAREP-39B. What is the address of register %rax?
QUESTION DATAREP-39C. Why might traversing a linked list be slower than traversing an array? List all that apply.
- A node in a linked list is larger than an element of an array, because the linked list node must also have pointers to its neighbors.
- Nodes in a linked list might be arranged in random order in memory, rather than sequentially, and sequential access is usually faster than random access.
- Traversing a linked list requires more instructions than traversing an array, and more instructions are always slower.
- Traversing a linked list just requires accessing memory, whereas traversing an array always require multiplication instructions to access elements by index, and multiplication is faster than memory access.
- None of the above.
QUESTION DATAREP-39D. List the typical segments of memory in increasing order by address on x86-64 Linux.
QUESTION DATAREP-39E. Give three different examples of types of undefined behavior.
QUESTION DATAREP-39F. Assuming that the following code does not execute undefined
behavior, what is the minimum value for N (the number of elements in
array a)?
int a[N];
int* x = a + 100;
x += 10;
int* y = &x[-5];
printf("%d value, %zd difference\n", *y, x - y);
DATAREP-40. Validity
You are helping Emily St. John Mandel debug her implementation of pset1. Her code includes the following global variables:
// Key: pointer to start of allocation
// Value: padded size of allocation in bytes
std::map<void*, size_t> active_allocs;
std::map<void*, size_t> freed_allocs;
const int MAGIC_FOUR_BYTE_VALUE = 0xABBACAFE; // For wild write detection
QUESTION DATAREP-40A. Emily’s code produces a segmentation fault in one of the tests.
A sanitizer run crashes on line 19 of an m61_insert_and_coalesce helper
function:
void m61_insert_and_coalesce(void* ptr, size_t sz) {
auto it = freed_allocs.lower_bound(ptr);
if (it != freed_allocs.begin()) {
--it;
}
if (it != freed_allocs.end() && (char*) it->first + it->second == (char*) ptr) {
// Coalesce down
it->second += sz;
} else {
// Can’t coalesce down, so insert
freed_allocs[ptr] = sz;
it = freed_allocs.find(ptr);
}
// Try coalescing up.
auto next = it;
++next;
if ((char*) it->first + it->second == next->first) {
it->second += next->second;
freed_allocs.erase(next);
}
}
What is the problem with Emily’s code? Describe how to fix it.
QUESTION DATAREP-40B. Having fixed that problem, she sees different sanitizer error
messages, on line 11 of m61_malloc.
void* m61_malloc(size_t sz, const char* file, int line) {
size_t padded_size = add_padding(sz);
assert(padded_size >= sz + 4 && padded_size % alignof(std::max_align_t) == 0);
void* ptr = m61_find_free_space(padded_size);
if (!ptr) {
return nullptr;
}
// Place magic_word after sz bytes to detect wild writes.
char* magic_ptr = (char*) ptr + sz;
*((int*) magic_ptr) = MAGIC_FOUR_BYTE_VALUE;
active_allocs[ptr] = padded_size;
return ptr;
}
What is the problem with Emily’s code? Describe how to fix it.
QUESTION DATAREP-40C. After resolving that problem, Emily observes that sometimes a
call to m61_free will corrupt a nearby allocation. For example:
size_t n = ...; /* some number > 0 */
void* a = m61_malloc(n);
memset(a, 'a', n);
void* b = m61_malloc(11);
memset(b, 'b', 11);
m61_free(a);
assert(memcmp(b, "bbbbbbbbbbb", 11) == 0); // Fails!
Here is her m61_free code. We’ve left out the code to detect invalid and
double frees, which is not relevant here.
void m61_free(void* ptr) {
// ... detect & handle `nullptr` and invalid and double frees ...
auto sz = active_allocs[ptr];
auto max_alignment = alignof(std::max_align_t);
size_t sz_plus_magic = sz + sizeof(int);
size_t padded_size = sz_plus_magic + max_alignment - (sz_plus_magic % max_alignment);
// Scribble over data to discourage use-after-free
memset(ptr, '!', padded_size);
active_allocs.erase(ptr);
freed_allocs.insert({ptr, padded_size});
}
Give a possible problem with Emily’s code, and describe how to fix it.
DATAREP-41. Internal metadata
The following internal metadata implementation places a header struct at the
start of every memory allocation. The payload (the space requested by the
user) immediately follows the header. MAGIC_ALLOC and MAGIC_FREE are
8-byte constants defined elsewhere.
struct header {
size_t magic; // MAGIC_ALLOC or MAGIC_FREE
size_t size; // Size of allocation, including padding and header
size_t prev_size; // Size of *previous* allocation; 0 if no previous allocation
size_t payload_size; // Size of payload (user-requested size)
char* file;
int line;
};
QUESTION DATAREP-41A. What is the alignment of the header struct?
QUESTION DATAREP-41B. What is the size of the header struct?
QUESTION DATAREP-41C. How many bytes of padding does the header struct contain, and
where?
QUESTION DATAREP-41D. Can the members of the header struct be rearranged at all to
make the struct smaller?
QUESTION DATAREP-41E. Assuming that the first header struct appears at the beginning
of default_buffer.buffer, how many bytes of padding are required after a
header struct to maintain correct alignment for user payloads?
QUESTION DATAREP-41F. Complete this function, which returns the payload pointer corresponding to a given header pointer.
void* header_to_payload(header* hdr) {
}
QUESTION DATAREP-41G. Complete this function, which returns the header pointer corresponding to a given payload pointer.
void* payload_to_header(void* payload) {
}
QUESTION DATAREP-41H. Complete this function, which given a header pointer hdr,
returns a pointer to the next allocation in default_buffer, or nullptr
if hdr is the last allocation in the buffer.
header* next_header(header* hdr) {
}
QUESTION DATAREP-41I. Complete this function, which given a header pointer hdr,
returns a pointer to the previous allocation in default_buffer, or
nullptr if hdr is the first allocation in the buffer.
header* previous_header(header* hdr) {
}
DATAREP-42. Invariants and allocators
Louise Bogan’s problem set 1 implementation uses external metadata. She has also written several data representation invariant checkers. Here are her data structures and checker functions.
struct allocation {
size_t size; // size requested by user
unsigned padding; // additional padding beyond `size`, e.g.,
// for boundary write detection and/or alignment
bool free; // true iff allocation is free
};
std::map<char*, allocation> allocs; // address -> allocation
void check_addresses_in_buffer() {
char* buf_first = default_buffer.buffer;
char* buf_last = buf_first + default_buffer.size;
for (auto& a : allocs) {
char* ptr = a.first;
assert(ptr != nullptr);
assert(ptr >= buf_first);
assert(ptr <= buf_last);
assert(ptr + a.second.size + a.second.padding <= buf_last);
}
}
void check_addresses_aligned() {
for (auto& a : allocs) {
uintptr_t addr = (uintptr_t) a.first;
assert(addr % alignof(std::max_align_t) == 0);
}
}
void check_sizes_valid() {
for (auto& a : allocs) {
assert(a.second.size + a.second.padding <= default_buffer.size);
}
}
void check_non_overlapping() {
char* last = default_buffer.buffer;
for (auto& a : allocs) {
char* ptr = a.first;
assert(ptr >= last);
last = ptr + a.second.size + a.second.padding;
}
}
void check_contiguous() {
char* last = default_buffer.buffer;
for (auto& a : allocs) {
char* ptr = (char*) a.first;
assert(ptr == last);
last = ptr + a.second.size + a.second.padding;
}
}
QUESTION DATAREP-42A. Some of these checker functions are redundant. (A checker
F is redundant when another checker, G, checks everything that F checks
and more.) List the redundant checker(s) and say which checkers they are
redundant with.
QUESTION DATAREP-42B. Add an assertion to the check_contiguous function that also
checks that the allocs map is complete, meaning that the entire space of
the default_buffer is included in allocs. Give the line number where the
assertion should go.
QUESTION DATAREP-42C. Write an assertion that would hold if Louise implements boundary
write detection, but would not necessarily hold if she did not. This
assertion could go in check_sizes_valid. Give the line number where the
assertion should go.
QUESTION DATAREP-42D. Louise’s m61_free, shown below, is meant to check for
invalid or double frees. Write an expression that evaluates to true on line
83 for most invalid or double frees (and never evaluates to true for
valid frees). The expression should use only the structures Louise already
defined.
void m61_free(void* ptr) {
if (ptr != nullptr) {
auto it = allocs.find((char*) ptr);
// ...Check for invalid or double free...
it->second.free = true;
}
}
QUESTION DATAREP-42E. Louise is currently using this function to make an allocation.
static char* find_allocation(size_t sz, size_t required_padding) {
assert((sz + required_padding) % alignof(std::max_align_t) == 0);
check_all_invariants(); // calls all checker functions
for (auto it = allocs.begin(); it != allocs.end(); ++it) {
// Is this allocation free & does it fit the space we need?
if (it->second.free && sz <= it->second.size) {
// Find this allocation’s boundaries
char* ptr = it->first;
char* end_ptr = ptr + it->second.size + it->second.padding;
// Split off the remaining space
char* split_ptr = ptr + sz + required_padding;
allocs.insert(it, {split_ptr, {end_ptr - split_ptr, 0, true}});
// Adjust current allocation
it->second.size = sz;
it->second.padding = required_padding;
it->second.free = false;
// Check invariants and return
check_all_invariants();
return ptr;
}
}
return nullptr;
}
She observes that when using this function, none of her invariants ever fail, but her allocator seems to grow slower and slower over time. For instance:
for (int i = 0; i != 1000000; ++i) {
void* ptr = m61_malloc(10);
m61_free(ptr);
}
void* ptr = m61_malloc(20); // This takes far longer than expected!
Why is this? Explain briefly, referring to specific lines in Louise’s code.
QUESTION DATAREP-42F. Suggest an invariant that would have caught this slowing-down problem and write a C++ assertion that would eventually fail with Louise’s problematic code. You can write a new assertion function or give a line number from the above assertions where the new assertion would go.
QUESTION DATAREP-42G. Louise also observes that when using her find_allocation
function, m61_malloc sometimes returns nullptr even when there should be
enough space available. For instance:
void* ptr1 = m61_malloc(1);
void* ptr2 = m61_malloc(default_buffer.size - 16);
assert(ptr1 && ptr2);
// The whole buffer is occupied, so any allocation will fail.
void* ptr3 = m61_malloc(2);
assert(!ptr3);
// After we free an allocation, though, there should be space—but there’s not!
m61_free(ptr1);
ptr3 = m61_malloc(2);
assert(ptr3); // Assertion fails!
Why is this? Explain briefly, referring to specific lines in Louise’s code.
QUESTION DATAREP-42H. Louise’s find_allocation has a “time bomb” in it—a problem
that doesn’t occur the way it is currently used, but that could occur if it
were called with valid, but unusual, arguments. Specifically,
find_allocation(1, 31) would cause a problem in some situations. Why is
this? Explain briefly, referring to specific lines in Louise’s code.
QUESTION DATAREP-42I. Write a checker function that checks that Louise’s allocations are completely coalesced, meaning that there are no adjacent free allocations.
![Data in cat[0]](../img/cat0.png)